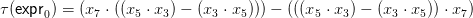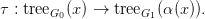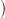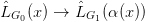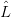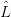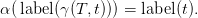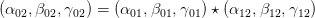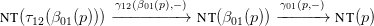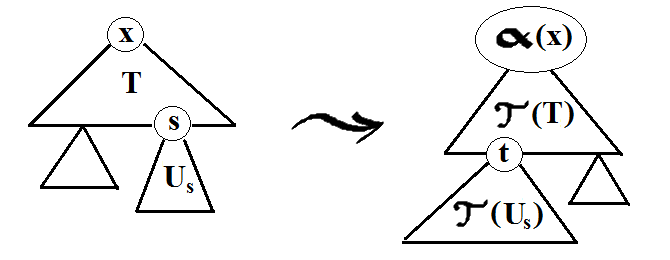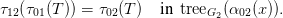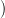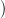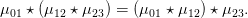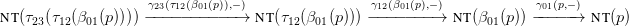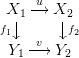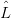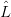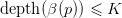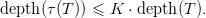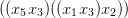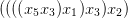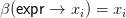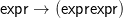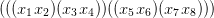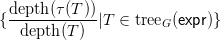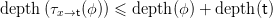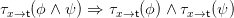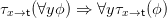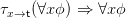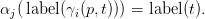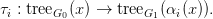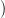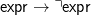Morphisms of context-free grammars
Tibor Beke
1. Introduction
Let me begin with a little known comment by Noam Chomsky (see [GE82] p.15 or [GE04] p.42), made
in response to a question on the significance of automata theory for linguistics and mathematics:
This seems to me what one would expect from applied mathematics, to see if you can
find systems that capture some of the properties of the complex system that you are
working with, and to ask whether those systems have any intrinsic mathematical interest,
and whether they are worth studying in abstraction. And that has happened exactly at
one level, the level of context-free grammar. At any other level it has not happened.
The systems that capture other properties of language, for example, of transformational
grammar, hold no interest for mathematics. But I do not think that is a necessary truth.
It could turn out that there would be richer and more appropriate mathematical ideas that
would capture other, maybe deeper properties of language than context free grammars do.
In that case you have another branch of applied mathematics which might have linguistic
consequences. That would be exciting.
Let me hasten to say that I do not wish to argue with Chomsky’s assessment. It would be hard to do, at
any rate, since he leaves room for both possibilities: that there is no linguistic theory beyond context-free
grammars that is of interest to mathematics; or perhaps there is. But I was particularly struck by the
sentence The systems that capture other properties of language, for example, of transformational
grammar, hold no interest for mathematics. From the 1970’s on, transformational grammar has been
responsible, directly on indirectly, for much research on generalizations of automata that, instead of
transforming strings to strings, transform trees to trees. Rational transducers, for example, gave rise to a
variety of tree transducers (deterministic, nondeterministic, top-down, bottom-up), in no small part
motivated by the desire to find a compact mathematical formalism underlying transformational
grammar. In fact, transformations of parse trees, called translations in the computer science
literature, are central to the contemporary theory of compilers. There has been a subtle change of
perspective, though. Transformational grammar, motivated by examples such as the English
passive, seeks to understand operations on tree-like structures within one given language.
Compilers translate from source code to object code: from one (typically context-free) language to
another.
One can appeal to an algebraic analogy at this point. If context-free languages are like algebras, then
context-free grammars are like presentations of algebras via generators and relations. One can map one
set of generators into another in a way that preserves relations; such a mapping induces a
homomorphism of algebras. So there ought to be such a thing as mapping one context-free grammar into
another in a ‘structure-preserving’ way, and this should induce a homomorphism between
languages.
The goal of this note is to give one possible definition of morphism of context-free grammars. This
notion will organize context-free grammars into a category [CWM] in such a way that the effects of
morphisms on parse trees — these are, more or less, the ‘translations’ of computer science — become
functorial. The appearance of these category-theoretic concepts is somewhat auxiliary, however, to the
main enterprise, which is to understand what it means to map one grammar into another ‘in a grammatical
way’.
We will be guided by four examples of grammatical operations. Keeping in mind Chomsky’s dictum,
each of them arises naturally within some body of formalized mathematics — algebra or logic. Going
through the motivating examples, the reader is invited to play with the following questions:
Which levels of the Chomsky hierarchy do the source and target languages belong to? Which
family of transformations (translations? transductions?) does the operation belong to? Each of
the motivating examples is given by an explicit formal recipe. Isn’t that recipe an outright
‘morphism’?
Motivating examples.
- In a (non-commutative) ring, the commutator [x,y] of two elements x,y is defined by
![[x,y] = x ⋅ y − y ⋅ x](beke_paper0x.png)
Let L0 be the language of well-formed iterated commutators of elements, and let L1 be
the language of well-parenthesized terms in the function symbols ⋅ and − . Consider the
operation that associates to an expression in L0 its equivalent in L1 (prior to expansion and
simplification). For example, [[x,y],z] is to be mapped to
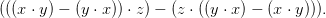
- Consider the language L0 of (ambiguous) parenthesis-free terms formed from a set of
variables with the binary operators ⊛ and ⊠. Let L1 be the language of terms, with the same
operators, in prefix form. Consider the multi-valued mapping that associates to a term in
L0 its prefix forms, under all possible parses. For example, the possible parses of x⊛y⊠z
are (using parentheses, informally)

or ⊠⊛ xyz resp. ⊛x ⊠ yz in prefix form.
Can this multi-valued mapping be described without mentioning prefix and infix traversals
of binary trees?
- Fix a first order signature, and consider the language L of well-formed formulas of first
order logic. Let x be a variable, t a term and ϕ a formula in L. Define the result τx→t(ϕ) of
replacing the free occurrences of x in ϕ by t by the usual set of rules. (These rules will not
be recalled here; see e.g. Mendelson [M10] or any careful textbook of logic.) Fix x and t,
and consider the map from L to itself sending ϕ to τx→t(ϕ).
- Consider again the language L of first order logic. The negation normal form, nnf(ϕ) of a
formula ϕ is defined by the rewrite rules
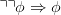
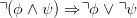
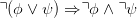
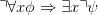
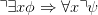
Iterated application of these rules transforms any well-formed formula into a logically
equivalent one where the targets of negation symbols (if any) are atomic formulas. Does
the operation sending ϕ to nnf(ϕ) belong in the same family as any of (a), (b) or (c)?
Notation. We will consider alphabets  and context-free grammars G with productions written x → s
where x ∈
and context-free grammars G with productions written x → s
where x ∈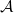 and s is a string in
and s is a string in 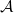 ∗. Neither
∗. Neither 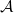 nor G is assumed finite. An element x of
nor G is assumed finite. An element x of 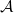 is non-terminal
if it occurs on the left-hand side of some production, and is terminal otherwise. N and T will denote the
set of non-terminal and terminal symbols, respectively; so
is non-terminal
if it occurs on the left-hand side of some production, and is terminal otherwise. N and T will denote the
set of non-terminal and terminal symbols, respectively; so 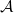 = N ⊔T . For u, v ∈
= N ⊔T . For u, v ∈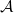 ∗, write u ⇒ v if v is
immediately derivable from u; let ⇒+ denote the transitive and ⇒∗ the reflexive-transitive closure of the
relation ⇒.
∗, write u ⇒ v if v is
immediately derivable from u; let ⇒+ denote the transitive and ⇒∗ the reflexive-transitive closure of the
relation ⇒.
We will find it convenient to consider each non-terminal as a possible start symbol, and to consider
strings both in the full alphabet 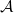 and in the set of terminals T . For x ∈ N, define
and in the set of terminals T . For x ∈ N, define
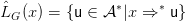
and
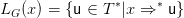
Thus, for non-terminal x, 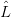 G(x) is the set of sentential forms that can be generated from x (considered as
a start symbol), and LG(x) is the usual language generated from x.
G(x) is the set of sentential forms that can be generated from x (considered as
a start symbol), and LG(x) is the usual language generated from x.
Let us recall the notion of unambiguous grammar in the form that will be most useful to
us:
This is equivalent to the requirement that the parse tree of every sentential form u ∈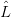 G(x) be unique;
or, equivalently, that there exist a unique leftmost derivation, starting from x, for each u ∈
G(x) be unique;
or, equivalently, that there exist a unique leftmost derivation, starting from x, for each u ∈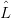 G(x). If every
non-terminal is productive, that is, LG(x) is non-empty for all non-terminals x, then Def. 1.1 is equivalent
to the unambiguity of the LG(x) in the classical sense. However, Def. 1.1 makes sense even if some or all
of the LG(x) are empty.
G(x). If every
non-terminal is productive, that is, LG(x) is non-empty for all non-terminals x, then Def. 1.1 is equivalent
to the unambiguity of the LG(x) in the classical sense. However, Def. 1.1 makes sense even if some or all
of the LG(x) are empty.
Definition 1.2. For x ∈ N, let tree G(x) denote the set of parse trees of sentential forms from
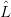 G(x), with root x. (One could just as well consider the set of leftmost or rightmost derivations,
or other representatives of equivalence classes of derivations, but the formalism of trees is the
handiest.) The depth of a tree is the number of nodes on the longest path from root to any leaf,
minus 1. Thus, for T ∈ tree G(x), depth(T) = 0 if and only if T consists solely of the root (which
is also a leaf) x. Note that depth(T) = 1 if and only if T equals some production x → s ∈ G.
Let nt(T) denote the set of leaves of T labeled by non-terminal symbols; for a node t of T , let
label(t) denote the label (i.e. element of the alphabet
G(x), with root x. (One could just as well consider the set of leftmost or rightmost derivations,
or other representatives of equivalence classes of derivations, but the formalism of trees is the
handiest.) The depth of a tree is the number of nodes on the longest path from root to any leaf,
minus 1. Thus, for T ∈ tree G(x), depth(T) = 0 if and only if T consists solely of the root (which
is also a leaf) x. Note that depth(T) = 1 if and only if T equals some production x → s ∈ G.
Let nt(T) denote the set of leaves of T labeled by non-terminal symbols; for a node t of T , let
label(t) denote the label (i.e. element of the alphabet 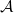 ) at t.
) at t.
Let T1 ∈ tree G(x) and let T2 be a tree with a leaf t such that label(t) = x. We will skip the
definition of the horticultural maneuver of grafting T1 onto T2 at the location t. It is the same as
the composition of (chains of) productions, as the illustration(s) below will make it clear.
2. Morphisms of grammars
Let G0 and G1 be context-free grammars in the alphabets 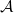 0 and
0 and 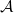 1, with terminals T0, T1 and
non-terminals N0, N1 respectively.
1, with terminals T0, T1 and
non-terminals N0, N1 respectively.
Definition 2.1. A morphism from G0 to G1 consists of the following data:
- a mapping α : N0 → N1
- a mapping β that assigns to each production x → s ∈ G0 an element of tree G1(α(x))
- for each production p ∈ G0, a function γ(p,−) from nt(β(p)) to nt(p), with the property
that for all t ∈ nt(β(p)),
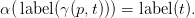
More plainly, α gives the translation of lexical categories. β specifies, for each production p : x → s in the
source grammar, a parse tree in the target grammar, with root α(x). Productions of the form x → s will be
translated to trees of the form β(x → s). The re-indexing map γ(p,−) associates to the location of each
non-terminal symbol r occurring as a leaf in β(x → s) the location of a non-terminal symbol s in s such
that α will translate s to r. This permits translation of the input parse tree by either top-down or bottom-up
recursion.
Let us make this more concrete by a formalization of our motivating example (a). For the sake of
readability, we will depart from the BNF convention of enclosing names of non-terminals in angle
brackets; strings typeset in sans serif font, such as var and expr, should be considered as stand-alone
symbols. Also, we will drop commas separating elements of a set being listed. Dots ‘…’ indicate a
(potentially infinite) set indexed by the natural numbers.
Example 2.2. Consider the source alphabet
| N0 | = {varexpr} | |
|
| T0 | = {[,]x1x2…xi…} | | |
Let the grammar
G0 consist of the productions
| var | → x1|x2|…|xi|… | |
|
| expr | → [var, var] | |
|
| expr | → [var, expr] | |
|
| expr | → [expr, var] | |
|
| expr | → [expr, expr] | | |
Now consider the target alphabet
| N1 | = {varexpr} | |
|
| T1 | = {() −⋅x1x2…xi…} | | |
Let the grammar
G1 consist of the productions
| var | → x1|x2|…|xi|… | |
|
| expr | → var − var|var ⋅ var | |
|
| expr | → var − (expr)|var ⋅ (expr) | |
|
| expr | → (expr) − var|(expr) ⋅ var | |
|
| expr | → (expr) − (expr)|(expr) ⋅ (expr) | | |
There is a morphism from G0 to G1 with components α,β,γ defined by
- α(expr) = expr and α(var) = var
- β(var → x) = x for any variable x; note that γ(var → x,−) has empty domain
- β(expr → [var, var]) is

generating the string (var ⋅ var) − (var ⋅ var). Let us refer to the leaves of the above tree via their
location in ‘(var ⋅ var) − (var ⋅ var)’; so the leaves labeled with non-terminals occur at {2, 4, 8, 10}.
Similarly, let us refer to the leaves in nt(expr → [var, var]) through their location in the string
‘[var, var]’, i.e. {2, 4}. Then define
| γ(expr → [var, var], 2) | = 2 | |
|
| γ(expr → [var, var], 4) | = 4 | |
|
| γ(expr → [var, var], 8) | = 4 | |
|
| γ(expr → [var, var], 10) | = 2 | | |
Visually, the re-indexing map γ(expr → [var, var],−) is indicated by the dotted and broken
arrows
![expr expr
| |
| |
[ varkkgg----,--- vareeee ] ( expr ) − ( expr )
----------------------- | |
-------- ------var ⋅ var var ⋅ ----var
---------- ----------
----------------------------------](beke_paper17x.png)
Continuing with the next production, define
![β(expr → [var,expr]) = (var ⋅ (expr)) − ((expr) ⋅ var)](beke_paper18x.png)
(Since G1 is unambiguous, we will identify sentential forms with their parse trees.) Using the
same coding of locations as above, define
| γ(expr → [var, expr], 2) | = 2 | |
|
| γ(expr → [var, expr], 5) | = 4 | |
|
| γ(expr → [var, expr], 10) | = 4 | |
|
| γ(expr → [var, expr], 13) | = 2 | | |
The treatment of the other two productions, and re-indexing of non-terminals therein, is
analogous.
How does translation from 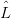 G0(expr) to
G0(expr) to 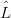 G1(expr) actually work? Consider a sentential form generated
by G0 from expr, say,
G1(expr) actually work? Consider a sentential form generated
by G0 from expr, say,
![[x7,[var,x3]]](beke_paper21x.png)
with parse tree
![expr
|
[ var , expr ]
|
|
x7 [ var , var ]
|
x3](beke_paper22x.png)
Since G1 is unambiguous, the process is easiest to describe by bottom-up induction. Starting from the
leaves, associate to each non-terminal symbol t in the input tree a string τ(t) from 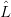 G1(α(x)):
G1(α(x)):
To see what is going on, let us affix subscripts to the non-terminals of the above parse tree:
![expr0
|
|
[ var0 , expr1 ]
|
x7 [ var1 , var2 ]
|
x|
3](beke_paper25x.png)
Then
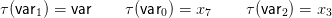
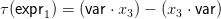

For the parse tree
![expr0
|
[ var , expr ]
0 | 1
|
x7 [ var1 , var2 ]
| |
x x
5 3](beke_paper29x.png)
a moment’s thought confirms that
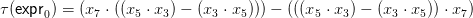
respecting all long-distance dependencies.
Above, G0 was an unambiguous grammar, hence one could talk of the translation of a string or of a
parse tree interchangeably. The next proposition defines the effect of a morphism of grammars in general.
We retain the notation of Def. 2.1.
Proposition 2.3. A morphism of grammars from G0 to G1 induces, for each x ∈ N0, a mapping
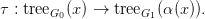
Indeed, for T ∈ tree G0(x), define τ(T) ∈ tree G1(α(x)) by induction on the depth of T :
∙ If depth(T) = 0, then T must be x itself, and τ(T) is defined to be α(x).
∙ If depth(T) > 0, let x → s ∈ G0 be the top production in T . Write p for x → s for brevity. Note that
nt(p) can be identified with a subset of s, namely, the locations of the non-terminal symbols in s.
Since G0 is context-free, each s ∈ nt(p) induces a subtree Ts of T with s as root. For each
t ∈ nt(β(p)), graft the tree τ(Tγ(p,t)) on β(p) with t as root. τ(T) is defined to be the resulting
tree.
The definition makes sense: since depth(Ts) < depth(T) for any s ∈ nt(p), τ(Ts) is defined by
the induction hypothesis. Note that τ(Ts) belongs to tree G1(α(label(s)) by the induction
assumption, and α label(γ(p,t))
label(γ(p,t))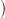 = label(t) by Def. 2.1. That is, the non-terminal symbol at
the root of τ(Tγ(p,t)) coincides with the non-terminal symbol at the location t. Since G1 is a
context-free grammar, the graft is well-defined, and τ(T) will belong to tree G1(α(x)) as desired.
□
= label(t) by Def. 2.1. That is, the non-terminal symbol at
the root of τ(Tγ(p,t)) coincides with the non-terminal symbol at the location t. Since G1 is a
context-free grammar, the graft is well-defined, and τ(T) will belong to tree G1(α(x)) as desired.
□
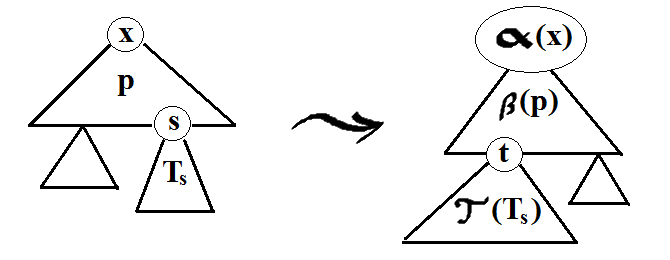
fig. 1: Computing τ(T). Above, p is a production (i.e. tree of depth 1), β(p) is a tree, s and t
are leaves labeled with non-terminal symbols such that s = γ(p,t). x and α(x) are the labels of
the roots.
Obviously, one can rewrite the above recursive definition into an algorithm to compute τ(T) by bottom-up
induction on T , from leaves toward the root. Note that if depth(T) = 1, that is, T is a production x → s in
G0, then τ(T) ends up being the same as β(T).
We will sometimes consider the induced translation τ as a multi-valued mapping
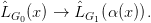
Indeed, for each u ∈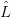 G0(x), there is a value for each parse tree T of u, namely, the string in
G0(x), there is a value for each parse tree T of u, namely, the string in 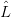 G1
G1 α(x)
α(x)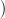 generated by τ(T).
generated by τ(T).
Proposition 2.4. For any x ∈ N0 and u ∈ LG0(x) with parse tree T , τ(T) generates a string in
LG1 α(x)
α(x)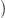 .
.
Proof. By induction on the depth of T . depth(T) = 0 is impossible, since x is assumed
non-terminal and u is a string of terminals. If depth(T) = 1, then T consists of the single
production x → u ∈ G0. The leaves of τ(x → u) = β(x → u) must consist of terminals.
Indeed, if there was a leaf labeled with a non-terminal, then γ(x → u,−) would need to map its
location to the location of some non-terminal in u, but u does not contain any non-terminals. So
τ(T) = β(x → u) generates a string in LG1 α(x)
α(x)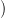 .
.
If depth(T) > 1, then τ(T) is, by the definition, the result of grafting trees of the form τ(Ts),
for subtrees Ts of T , onto those leaves of β(x → s) that contain non-terminals. Using the induction
hypothesis, all leaves of τ(Ts) are labeled with terminal symbols; hence τ(T) generates an element
of LG1 α(x)
α(x) as well. □
as well. □
Let us summarize the discussion so far:
Example 2.6. Returning to our motivating example (b), consider the source alphabet
| N0 | = {expr} | |
|
| T0 | = {⊛⊠x1x2…xi…} | | |
Let the grammar
G0 consist of the productions
| expr | → x1|x2|…|xi|… | |
|
| expr | → expr ⊛ expr | |
|
| expr | → expr ⊠ expr | | |
Now consider the target grammar G1 with identical alphabet N1 = N0, T1 = T0 but
productions
| expr | → x1|x2|…|xi|… | |
|
| expr | →⊛exprexpr | |
|
| expr | →⊠exprexpr | | |
There is a morphism from G0 to G1 with components α,β,γ defined by
- α(expr) = expr
- β(expr → x) = x for any variable x; note that γ(expr → x,−) has empty domain
- β(expr → expr ⊛ expr) = ⊛exprexpr with γ(2) = 1 and γ(3) = 3
- β(expr → expr ⊠ expr) = ⊠exprexpr with γ(2) = 1 and γ(3) = 3
(Since G1 is unambiguous, there is no loss in writing the values of β as strings, as opposed to parse trees.
The first argument of γ is suppressed for the sake of readability; numbers refer to locations of
non-terminal symbols, as before.) For any u ∈ LG0(expr), the values of τ(u) will be the prefix forms of the
parses of u.
Before moving on to compositions of morphisms and the rest of our motivating examples, let us make a
series of remarks.
∙ The definition of morphism of grammars, as given above, appears out of the blue, and in somewhat
austere generality. Admittedly, the definition, like most in the realm of algebra, is ‘experimental’, and
driven by several, not easily formalizable criteria. It should cover enough cases of interest, seemingly not
otherwise connected; it should possess good structural properties; and should have a family, or conceptual
resemblance to other notions that have proved useful. As for the instances of morphisms of grammars in
mathematical syntax, I am hopeful this article provides quite a few. The desired structure theory is phrased
in the language of categories; see below. As for family resemblances, there exist significant overlaps
between the formalisms of tree transducers, term rewrite systems and context-free language
transformations, discussion of which would take us far afield. Suffice it to say that the notion of
morphism of grammars is most similar to (and in fact, properly contains) synchronous context-free
grammars (SCFG); see e.g. Chapter 23 of [AS10]. SCFG are themselves notational variants of the
syntax-directed translation schemata of Aho and Ullman [AU72]. The differences are quite significant:
- unlike SCFG, morphisms assume the existence of source and target grammars, their
alphabets linked by a map α
- SCFG pair rules with rules; morphisms associate to each rule in the source grammar a parse
tree in the target grammar
- in a SCFG, each re-indexing map is a permutation of non-terminal symbols; in a morphism,
the re-indexing datum γ(x → s,−) is a map from the locations of non-terminal symbols
in β(x → s) to the locations of non-terminal symbols in s.
Thus, because of the presence of repeated variables, our motivating example (a) could not be handled by a
SCFG. Nonetheless, it is fair to think of morphisms of grammars as syntax-directed translation schemes,
boosted to their ‘natural level of generality’.
∙ Recall that our grammars do not contain preferred start symbols; a morphism of grammars induces a
multi-valued map
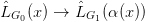
for each non-terminal x in the alphabet 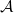 0 of G0. It may well happen that for some u ∈
0 of G0. It may well happen that for some u ∈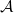 0∗, there exist
distinct x0,x1 ∈ N0 such that u ∈
0∗, there exist
distinct x0,x1 ∈ N0 such that u ∈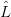 G0(x0) and u ∈
G0(x0) and u ∈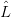 G0(x1), and the translation(s) into
G0(x1), and the translation(s) into 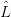 G1
differ when u is considered as a descendant of x0 from when it is considered a descendant of
x1.
G1
differ when u is considered as a descendant of x0 from when it is considered a descendant of
x1.
∙ The language of iterated commutators, cf. Example 2.2, could be more succinctly defined with the
help of a single non-terminal symbol expr and productions
| expr | → x1|x2|…|xi|… | |
|
| expr | → [expr, expr] | | |
However, as long as one prefers to put parentheses around compound expressions, but not around
individual variables in the language of terms with infix operators − and ⋅, one needs both of the syntactic
categories var and expr in the target language. This, in turn, necessitates that the source language
should distinguish variables from compound expressions; hence the more labored grammar
G0 of Example 2.2. This observation highlights that our morphisms are defined between
context-free grammars, and are sensitive to the choice of grammar, even for unambiguous
languages.
∙ What seems to be conspicuously missing from the definition of morphism is how the terminal
symbols get translated. Indeed, the function α that is part of the morphism data goes from non-terminal
symbols to non-terminal symbols. Of course, the function β is responsible for the translation of terminals,
since terminals occurring in the language can be reached from the source non-terminal via productions. In
fact, the reader may enjoy working the following out. Let T0, T1 be alphabets. Recall that any map
h : T0 → T1∗ induces a semigroup homomorphism h : T
0∗ → T
1∗. (The reuse of the letter ‘h’ should
cause no confusion.) For a language L ⊆ T0∗, h restricts to a map h : L → T
1∗. Maps of this type are
called literal homomorphisms.
Exercise. Let G0 be a context-free grammar in the alphabet N0 ⊔ T0 and T1 another set of terminals.
Let h : T0 → T1∗ be a map, inducing a literal homomorphism h : L
G0(x) → T1∗ for each x ∈ N
0.
Show that there exists a context-free grammar G1 in the alphabet N0 ⊔ T1 and a morphism of
grammars G0 → G1 whose associated translation τ : LG0(x) → LG1(x) is single-valued
and satisfies τ(u) = h(u) for all u ∈ LG0(x), any x ∈ N0. (Hint: extend h to a semigroup
homomorphism (N0 ⊔ T0)∗ → (N
0 ⊔ T1)∗ by setting h(x) = x for x ∈ N
0. α is the identity. Now let
β(x → s) = h(s).)
That is, any literal homomorphism can be induced by a morphism of grammars. Similarly,
any rational transducer (thought of as a multi-valued mapping from its domain to its range,
both being rational languages) can be encoded via a morphism of grammars. The details of
this encoding are straightforward, but will be skipped here. It is unlikely that the notion of
morphism of grammars will have anything to add to the very fine-tuned theory of rational
transducers.
The next proposition is a simultaneous extension of Prop. 2.4 and of the defining property of the
re-indexing map γ from the definition of morphism.
Proposition 2.7. Let (α,β,γ) be a morphism of context-free grammars from G0 to G1, x ∈ N0
and T ∈ tree G0(x). There is a natural map γ(T,−) from nt(τ(T)) to nt(T) such that for any
t ∈ nt(τ(T)),
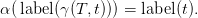
Proof. By induction on the depth of T . If depth(T) = 0 then T consists of just the root
x ∈ N0, and τ(T) is the tree containing only the root α(x) ∈ N1. So nt(T) = {x} and
nt(τ(T)) = {α(x)}; γ(T,−) is uniquely determined.
If depth(T) > 0, recall how τ(T) is defined. Let p ∈ G0 be the top production in T . As before,
this induces subtrees Ts of T with roots s ∈ nt(p). For each t ∈ nt(β(p)), graft the tree τ(Tγ(p,t))
on β(p) with t as root. τ(T) is defined to be the resulting tree.
Consider any t ∈ nt(β(p)) and let s = γ(p,t). Since depth(Ts) < depth(T), by the induction
hypothesis there is a map γ(Ts,−) from nt(τ(Ts)) to nt(Ts), with α as left inverse to the action
of γ(Ts,−) on labels. When grafting τ(Ts) to β(p), the domain of γ(Ts,−) can be shifted with it,
to become a subset of nt(τ(T)).
However, nt(τ(T)) is the disjoint union of the various nt(τ(Ts)) grafted to β(p), with
s = γ(p,t), as t ranges over nt(β(p)). γ(T,−) can thus be defined as the disjoint union of the
(appropriately shifted) maps γ(Ts,−). □
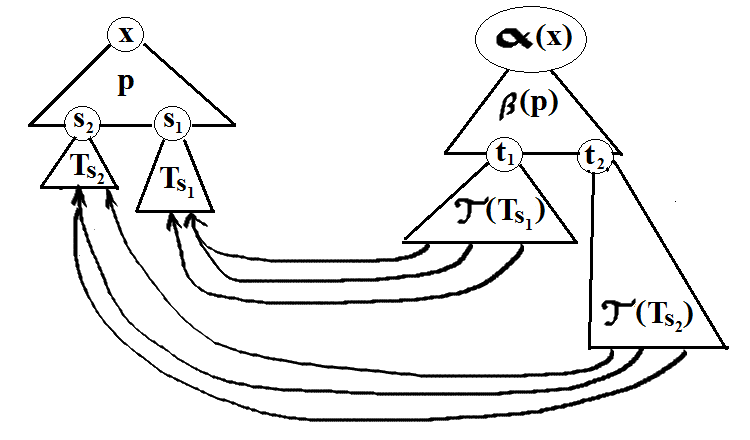
fig. 2: Defining γ(T,−). Above, p is a production (i.e. tree of depth 1), β(p) is a tree, s1,s2,t1
and t2 are leaves labeled with non-terminal symbols such that s1 = γ(p,t1) and s2 = γ(p,t2).
Note that if T is a production x → s ∈ G0 then γ(T,−), as constructed above, coincides with
γ(x → s,−) that is part of the morphism data; there is thus no conflict of notation.
Observe also that when T is a parse tree of some string u containing only terminal symbols then the
leaves of τ(T) cannot contain non-terminals either (since no map γ(T,−) with the properties above could
exist); so we indeed have an extension of Prop. 2.4.
Our choice of terminology insinuates that morphisms can be composed, and, with context-free
grammars as objects, form a category. We will treat this next.
Definition 2.8. Let G0,G1,G2 be context-free grammars, and let (α01,β01,γ01) be a morphism
from G0 to G1, and (α12,β12,γ12) a morphism from G1 to G2. Define their composite
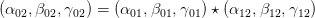
a morphism from G0 to G2, as follows:
α02 is the composite N0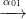 1
1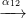 2.
2.
Let x → s (abbreviated as p) be a production in G0. Set β02(p) = τ12 β01(p)
β01(p) , where τ12 is
the induced translation from tree G1(y) to tree G2
, where τ12 is
the induced translation from tree G1(y) to tree G2 α12(y)
α12(y)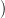 , for y ∈ N1. Note that β02(x → s) is
an element of tree G2(α12(α01(x))), i.e. of tree G2(α02(x)), as required.
, for y ∈ N1. Note that β02(x → s) is
an element of tree G2(α12(α01(x))), i.e. of tree G2(α02(x)), as required.
γ02(p,−) is to be a map from nt(β02(p)) to nt(p). It is defined as the composite
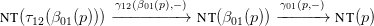
More plainly, a production p ∈ G0 is translated by β01 into a parse tree T1 formed with G1, which τ12
translates into a parse tree T2 formed with G2. The re-indexing map γ12(β01(p),−) goes from
leaves of T2 labeled with non-terminal symbols to leaves of T1 labeled with non-terminal
symbols, followed by the re-indexing map γ01(p,−) from leaves of T1 labeled with non-terminal
symbols, to leaves (i.e. letters on the right-hand side) of the production p that are non-terminal
symbols.
As a continuation of Example 2.6, it is instructive at this point to construct grammars G0, G1,
G2 for prefix resp. postfix resp. fully parenthesized infix terms of binary function symbols
⊛ and ⊠, and morphisms Gi → Gj (i,j ∈{0, 1, 2}) that form a commutative diagram of
isomorphisms. Of course, one expects more: a commutative diagram of (iso)morphisms of
grammars should induce a commutative diagram of (bijective) mappings between the associated
languages. That is indeed so. To prove it, we need a key structural property of τ. By definition,
the translation τ(T) of a parse tree T can be generated by attaching to the translation of the
top production in T the translations of the sub-trees of the top production — appropriately
re-indexed. The next lemma states that the same recipe applies if one separates any top segment, not
necessarily just the top production, of the input tree. The necessary re-indexing is supplied by
Prop. 2.7.
Lemma 2.9. Let x ∈ N0 and T ∈ tree G0(x). For each s ∈ nt(T), suppose given Us ∈
tree G0(label(s)). Let TU ∈ tree G0(x) be the result of grafting each Us to s as root. Now, for
each t ∈ nt(τ(T)), graft τ(Uγ(T,t)) to τ(T) with t as root. Let τ(T)τ(U) ∈ tree G1(α(x)) be the
resulting tree. Then τ(TU) = τ(T)τ(U).
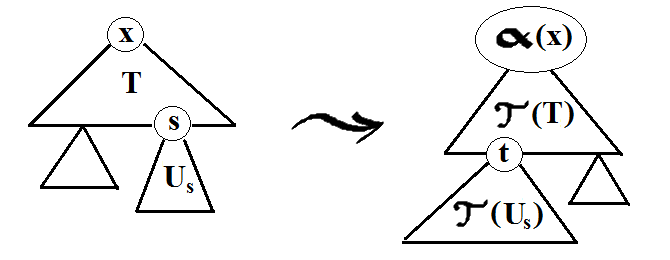
fig. 3: Modularity of τ(T). s and t are leaves labeled with non-terminal symbols
such that s = γ(p,t). x and α(x) are labels of the roots. Note the similarity with
Fig. 1.
Proof. By induction on depth(T). When depth(T) = 0, the lemma is a tautology. When
depth(T) = 1, it is the inductive step in the definition of τ (applied to the tree TU, whose top
production is T ).
If depth(T) > 1, let p ∈ G0 be the top production in T . As before, this induces subtrees Tr
of T with roots r ∈ nt(p). The set of leaves of T with non-terminal labels, nt(T), is the disjoint
union of nt(Tr) as r ranges over nt(p). For each r ∈ nt(p), let Tr,U be the tree that results from
grafting Us to s for each s ∈ nt(Tr). Tr,U is thus the same as the subtree of TU with r as root.
τ(TU) (by the inductive step in the definition of τ) is the result of grafting τ(Tγ(p,v),U)
to v, for v ranging over nt(β(p)). Pick such a v ∈ nt(β(p)) and let r = γ(p,v). Since
depth(Tr,U) < depth(T), by the induction hypothesis τ(Tr,U) is the same as the result of grafting,
for each t ∈ nt(τ(Tr)), τ(Uγ(Tr,t)) to t as root. As v ranges over nt(β(p)), this assembles to
the same tree as τ(T) with τ(Uγ(T,t)) grafted to t for each t ∈ nt(τ(T)). But that is the same as
τ(T)τ(U) by definition, completing the induction step. □
Proposition 2.10. If G0, G1, G2 are context-free grammars and (α01,β01,γ01) : G0 → G1
resp. (α12,β12,γ12) : G1 → G2 morphisms of grammars, with composite (α02,β02,γ02) : G0 →
G2 and associated translation functions τ01,τ12 and τ02. Then for all x ∈ N0 and T ∈ tree G0(x),
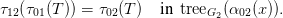
Proof. When depth(T) = 0, this reduces to α12 α01(x)
α01(x)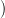 = α02(x). When depth(T) > 0, let
p be the top production in T , inducing subtrees Ts with roots s ∈ nt(p) as before. τ01(T), by
definition, is the result of grafting τ01(Tγ01(p,t)) to t for each t ∈ nt(β01(p)). τ12 of that composite
tree, by Lemma 2.9, is the result of grafting τ12
= α02(x). When depth(T) > 0, let
p be the top production in T , inducing subtrees Ts with roots s ∈ nt(p) as before. τ01(T), by
definition, is the result of grafting τ01(Tγ01(p,t)) to t for each t ∈ nt(β01(p)). τ12 of that composite
tree, by Lemma 2.9, is the result of grafting τ12 τ01(Tγ01(p,t))
τ01(Tγ01(p,t))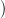 , with t = γ12(τ12(β01(p)),r), to
r ∈ nt(τ12(β01(p))). But that is the same as the translation of T under τ02, by definition of the
composite of two morphisms. □
, with t = γ12(τ12(β01(p)),r), to
r ∈ nt(τ12(β01(p))). But that is the same as the translation of T under τ02, by definition of the
composite of two morphisms. □
Proposition 2.11. The composition of morphisms of context-free grammars is associative. That
is, if Gi (i = 0, 1, 2, 3) are context-free grammars, and μi,i+1 = (αi,i+1,βi,i+1,γi,i+1) morphisms
from Gi to Gi+1 (here i = 0, 1, 2) then
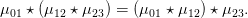
Definition 2.12. Let cfg be the category whose objects are context-free grammars, with
morphisms defined by Prop. 2.1 and composition defined by Prop. 2.8. The identity morphism on
G is given by (id N, id G, id nt(p)), i.e. identity maps.
We are now ready to assemble Prop. 2.3, Cor. 2.5, Prop. 2.10 and Prop. 2.11 into the main theorem of
this paper. Intuitively, it says that tree is a functor from cfg to the category of sets. However,
since we did not include a preferred start symbol in the data for context-free grammars (and
much less did we assume that any such symbol would be preserved by morphisms), the target
category is slightly more complicated. Let Mor(Set) be the category of maps of sets. An
object of Mor(Set) is thus a function f : X → Y between arbitrary sets; a morphism from
f1 : X1 → Y 1 to f2 : X2 → Y 2 consists of maps u : X1 → X2 and v : Y 1 → Y 2 such
that
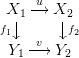
commutes. Morphisms are composed ‘horizontally’. Mor(Set) is an example of a diagram category (see
e.g. MacLane [CWM]), but an alternative way to think of it is as the category of sets fibered over a base:
f : X → Y can be thought of as the family of sets f−1(y) with y ∈ Y . Morphisms are then fiberwise
maps.
There exists a well-understood interplay between rational languages, finite state automata, and monoid
objects in categories; the canonical reference is Arbib [AA69]. Category-theoretic properties of cfg (for
example, the existence of pullbacks, filtered colimits or coproducts) as well as the roles that morphisms,
functors, natural transformations etc. may play in formal language theory at higher levels of the Chomsky
hierarchy, are much less explored.
3. Looking ahead
We have only dealt with two of the motivating examples. Neither of the other two can be described by a
morphism G → G where G is any of the usual unambiguous context-free grammars for first order logic,
or, I suspect, any context-free grammar for it. It should come as no surprise that there are limitations to the
‘word processing power’ of morphisms, as defined above. One expects that there exists a hierarchy of
mappings between context-free grammars, just as there are hierarchies of languages, complexity
classes, and so on. The goal of this final — much more speculative — section is to sketch
further levels of this hierarchy. But first, here is one expression of the structural limitations of
morphisms.
Proposition 3.1. Suppose (α,β,γ) : G0 → G1 is a morphism of grammars with the property that
for some constant K,
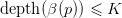
for all p ∈ G0. Then for all x ∈ N0 and T ∈ tree G0(x),
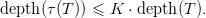
The proof is by induction on depth(T). Note that such a bound K always exists if G0 is finite; however,
our grammars (and alphabets) were not assumed to be so by default.
Example 3.2. Let L be the language of function terms for an associative binary operation (denoted by
juxtaposition), fully parenthesized, with infinitely many variables available. The alphabet
is
| N | = {expr} | |
|
| T | = {()x1x2…xi…} | | |
with unambiguous grammar
| expr | → x1|x2|…|xi|… | |
|
| expr | → (exprexpr) | | |
Let
τ : L → L be the mapping that sends an expression to its leftmost-parenthesized equivalent. For
example,
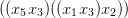
is to be sent to
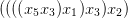
If there was a morphism of grammars (α,β,γ) : G → G inducing τ, it would have to satisfy
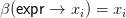
for all i = 1, 2,…. Since there is only one other production in the grammar, namely,
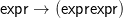
Prop. 3.1 would apply. However, for any positive integer d, let T be the term in variables
x1,x2,…,x2d whose parse tree (ignoring parentheses) is the complete binary tree of depth d; e.g. for
d = 3:
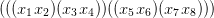
τ(T) is a left-branching tree, with depth 2d.
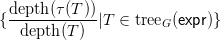
is thus unbounded, and the mapping τ cannot correspond to any morphism of grammars.
This argument does not apply to our motivating example (c), replacement of free occurrences of a
variable x in the input formula ϕ by some term t, since
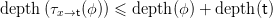
always. (We have silently fixed an unambiguous context-free grammar G for first order logic.) However,
no morphism G → G induces τx→t(ϕ). The recursive rules
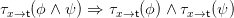
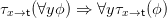
showing that replacement descends the parse tree along boolean connectives and quantification with
respect to variables other than x, conform perfectly to the combinatorial possibilities of a self-morphism
of G. However, one has
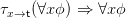 | (∗) |
since all free occurrences of x in ϕ become bound in ∀xϕ. τx→t(∀xϕ) is thus not a function of τx→t(ϕ),
since ϕ cannot in general be reconstructed from τx→t(ϕ). So τx→t cannot be computed by bottom-up
induction, whereas translations induced by morphisms can always be.
Intuitively, a morphism of grammars applies the same functional transformation (itself!),
iteratively, to subtrees of the input tree, whereas (∗) calls on a different transformation (namely, the
identity) when the input has the form ∀xϕ. Recall that two functions f,g : ℕ → ℕ are defined by
simultaneous recursion if f(0) and g(0) are given, and there exist functions F and G such that for
n > 0,
| f(n) | = F n,f(n − 1),g(n − 1) n,f(n − 1),g(n − 1)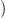 | |
|
| g(n) | = G n,f(n − 1),g(n − 1) n,f(n − 1),g(n − 1)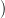 . . | | |
In the presence of a pairing function that codes the ordered pair ⟨f(n),g(n)⟩ as a single natural
number, simultaneous recursion can be replaced by ordinary recursion. However, for tree
transformations, simultaneous recursion on syntax has more expressive power than simple
recursion.
Definition 3.3. Let G0 and G1 be context-free grammars in the alphabets N0,T0, N1,T1 as usual, and k
a positive integer. A k-morphism from G0 to G1 defined by simultaneous recursion consists of the
following data:
- mappings αi : N0 → N1 for i = 1, 2,…,k
- mappings βi, for i = 1, 2,…,k, assigning to each production x → s ∈ G0 a parse tree from
tree G1(αi(x))
- for each i = 1, 2,…,k and each production p ∈ G0, a function γi(p,−) from nt(βi(p)) to
nt(p) and a function δi(p,−) from nt(βi(p)) to {1, 2,…,k}, with the property that for all
i = 1, 2,…,k and all t ∈ nt(βi(p)), writing j = δi(p,t),
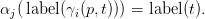
A k-morphism is, roughly, a k-tuple of grammatical transformations that are intertwined via the
function δ: the i-th transformation can call on the j-th transformation to act on a subtree of the input tree.
The maps αi provide the initial values. There is no circular dependency, since each recursive call applies
to a lower-level subtree of the input tree. More precisely,
Proposition 3.4. A k-morphism of grammars from G0 to G1 induces, for each i = 1, 2,…,k and
x ∈ N0, a mapping
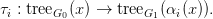
Proof. For T ∈ tree G0(x), define the τi(T) ∈ tree G1(αi(x)) simultaneously by induction on the
depth of T :
∙ If depth(T) = 0, then T must be x itself, and τi(T) is defined to be αi(x).
∙ If depth(T) > 0, let x → s ∈ G0 be the top production in T . Write p for x → s for brevity.
As usual, nt(p) can be identified with a subset of s, the locations of the non-terminal symbols in
s. Since G0 is context-free, each s ∈ nt(p) induces a subtree Ts of T with s as root. For each
i = 1, 2,…,k and t ∈ nt(βi(p)), writing j = δi(p,t), graft the tree τj(Tγi(p,t)) on βi(p) with t as
root. τi(T) is defined to be the resulting tree.
Since depth(Ts) < depth(T) for all s ∈ nt(p), τj(Ts) is defined by the induction
hypothesis. Note that τj(Ts) belongs to tree G1(αj(label(s)) by the induction assumption, and
αj label(γi(p,t))
label(γi(p,t))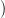 = label(t) by Def. 3.3. That is, the non-terminal symbol at the root of
τj(Tγi(p,t)) coincides with the non-terminal symbol at the location t. Since G1 is a context-free
grammar, the graft is well-defined, and τi(T) will belong to tree G1(αi(x)) as desired. □
= label(t) by Def. 3.3. That is, the non-terminal symbol at the root of
τj(Tγi(p,t)) coincides with the non-terminal symbol at the location t. Since G1 is a context-free
grammar, the graft is well-defined, and τi(T) will belong to tree G1(αi(x)) as desired. □
When finding τi(T) by recursion from root to leaves on T , one can restrict to computing τj(Ts) only
for those subtrees Ts of T and values j ∈{1, 2,…,k} that are called for by the indexing function δ. When
using bottom-up induction, the entire k-tuple of values  τ1(−),τ2(−),…,τk(−)
τ1(−),τ2(−),…,τk(−)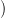 needs to be computed
for all subtrees of T .
needs to be computed
for all subtrees of T .
Mutatis mutandis, the results of the previous section, from Prop. 2.3 to Prop. 3.1, remain valid for
morphisms defined by simultaneous recursion. The composition of a k-morphism from G0 to G1 and
n-morphism from G1 to G2 will be a k ⋅ n-morphism from G0 to G2. Composition is associative,
and tree G becomes a functor from cfg to tuples of functions of sets. The details, while not
conceptually complicated, are quite tedious (largely for notational reasons) and will not be needed
here.
The reader is invited to define the pair of transformations (τx→t, id) by simultaneous recursion on the
syntax of first order logic. τx→t calls itself and id, while the identity transformation calls itself only. The
fact that the treatment of descendant nodes is inherited from their parent nodes is reminiscent of attribute
grammar.
Note that ϕx→t, replacing all free occurrences of the variable x in the formula ϕ by the term t, is the
least complicated of the multitude of operations involving variable replacement and binding. If a
free variable in t is captured by a quantifier in ϕ, then ϕ will no longer imply its instance
ϕx→t; to preserve the intended logical meaning, the dummy variable appearing in the capturing
quantifier in ϕ should be renamed first, to a variable not occurring in ϕ or t. However, the function
that returns a variable not occurring in a given formula does not have a canonical value, and
is not easily describable in terms of language operations. A related, and much researched,
issue is the formalization of explicit substitution in lambda calculi [ES90]: under explicit
substitution, the operation x → t does not belong to the meta-language, but is part of the language
itself. On the other hand, there seem to exist few studies, from the viewpoint of mathematical
linguistics, of the syntax of substitutions through de Bruijn indices or Bourbaki’s variable-free
notation [TL99].
Prop. 3.1 does not apply either to our fourth (and last) motivating example, transforming first order
formulas ϕ to negation normal form nnf(ϕ), since depth(nnf(ϕ)) ≤ depth(ϕ) always. But nnf cannot
be induced by a morphism, or in fact k-morphism. The standard context-free grammars of first order logic
contain the production
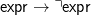
But β(expr →⌝expr) cannot contain any terminal symbols; any non-terminal other than ‘expr’; or more
than one copy of ‘expr’: each of those possibilities would be inconsistent with the fact that
nnf(⌝⌝ϕ) = nnf(ϕ). So β(expr →⌝expr) is forced to be ‘expr’, which of course is incompatible with the
negation normal form of ⌝ϕ for atomic ϕ.
Intuitively, the issue is that the rewrite rules
| ⌝⌝ϕ | ⇒ϕ | |
|
| ⌝(ϕ ∧ ψ) | ⇒⌝ϕ ∨⌝ψ | |
|
| ⌝(ϕ ∨ ψ) | ⇒⌝ϕ ∧⌝ψ | |
|
| ⌝∀xϕ | ⇒∃x⌝ψ | |
|
| ⌝∃xϕ | ⇒∀x⌝ψ | | |
may introduce new instances of the negation symbol on their right hand sides. It requires a moment of
thought to verify that this set of rules is noetherian (starting with any formula, they cannot be applied
infinitely often) and many more moments of thought to verify that they are confluent (every formula has a
unique negation normal form, even if the above rewrite rules are applied to arbitrary subformulas first, in
any order, until no rule applies anywhere).
Recall that a term rewrite system (TRS) is an unordered set of rewrite rules acting on function terms in
some fixed signature. A TRS is called convergent if it is both noetherian and confluent [TR98].
All four motivating examples, and Example 3.2 as well, belong to the family of convergent
TRS, adapted from the unambiguous grammar of function terms to the general setting of
context-free grammars. The fact that the effect of morphisms on parse trees can be computed by
both bottom-up and top-down recursion, as well as Lemma 2.9, can be seen as corollaries of
confluence.
It is quite challenging, however, to fashion a category out of convergent TRS. To begin with, neither the
confluence nor the noetherianness of TRS is, in general, decidable (though, curiously, the confluence of
noetherian TRS is decidable). Secondly, a famous example due to Toyama shows that the disjoint union of
two convergent TRS need not be convergent. Thus the composite of two TRS cannot, in general, be
defined as the disjoint union of their underlying rules. There exist, however, sufficient conditions
for the modularity of convergence for TRS. Alternatively, one can experiment with ordered
(prioritized) rewriting rules.
In a different direction, the notion of morphism of context-free grammars could be broadened to allow
for non-determinism: several right-hand sides of the component β. Finally, the focus on parse trees is, to
some extent, restrictive: the domain of these transformations could be any set of node-labeled rooted trees
closed under taking subtrees.
I hope to elaborate some of these ideas in later publications. In closing, let me return to the
quote from Chomsky that opened this article. Suppose that the only gift linguistics ever gave
mathematics was, indeed, the notion of context-free grammar. Let’s play with this present: expand
the focus from context-free grammars to maps of context-free grammars (from objects to
morphisms) and I think we will agree that linguistics has given mathematics a gift that keeps on
giving.
References
[AA69] M. Arbib: Theories of abstract automata. Prentice–Hall, 1969
[AS10] Algorithms and Theory of Computation Handbook. Vol 2: Special Topics and Techniques. Ed. by
M. Atallah and M. Blanton. 2nd ed., Chapman & Hall, 2010
[AU72] A. Aho and J. Ullman: The Theory of Parsing, Translation, and Compiling. Vol 1: Parsing.
Prentice–Hall, 1972
[CWM] S. MacLane: Categories for the Working Mathematician. 2nd ed., Springer–Verlag, 1998
[ES90] M. Abadi, L. Cardelli, P.-L. Curien, J.-J. L\E9vy: Explicit substitutions. Digital Systems Research Center
Technical Report SRC-RR-54, 1990
[GE82] Noam Chomsky on The Generative Enterprise: A Discussion with Piny Huybregts and Henk van
Riemsdijk, Foris Publications, Dordrecht–Holland 1982
[GE04] The Generative Enterprise Revisited: Discussions with Riny Huybregts, Henk Van Riemsdijk, Naoki
Fukui, and Mihoko Zushi. With a New Foreword by Noam Chomsky. de Gruyter, 2004
[M10] E. Mendelson: Introduction to Mathematical Logic. 5th edition, Chapman & Hall, 2010
[TL99] A.R.D. Mathias: A term of length 4,523,659,424,929. Preprint, 1999
Available at www.dpmms.cam.ac.uk/~ardm/inefff.pdf
[TR98] F. Baader and T. Nipkow: Term Rewriting and All That. Cambridge University Press, 1998
Department of Mathematics, University of Massachusetts, Lowell, One University Avenue,
Lowell, MA 01854
E-mail address: tibor_beke@uml.edu
![[x,y] = x ⋅ y − y ⋅ x](beke_paper0x.png)
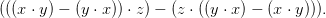

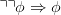
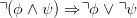
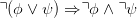
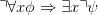
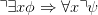
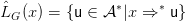
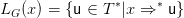
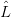
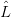
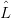
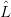
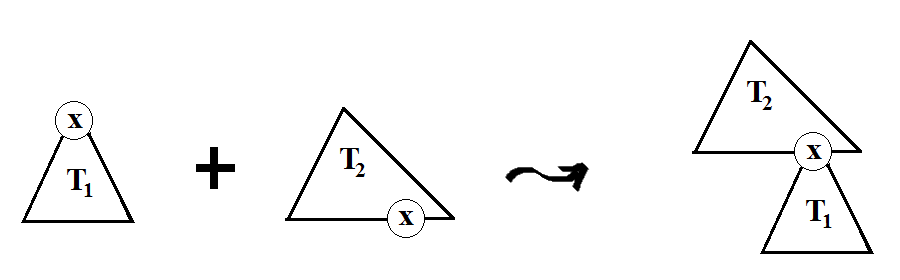

![expr expr
| |
| |
[ varkkgg----,--- vareeee ] ( expr ) − ( expr )
----------------------- | |
-------- ------var ⋅ var var ⋅ ----var
---------- ----------
----------------------------------](beke_paper17x.png)
![β(expr → [var,expr]) = (var ⋅ (expr)) − ((expr) ⋅ var)](beke_paper18x.png)
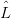
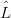
![[x7,[var,x3]]](beke_paper21x.png)
![expr
|
[ var , expr ]
|
|
x7 [ var , var ]
|
x3](beke_paper22x.png)
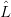
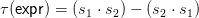
![expr0
|
|
[ var0 , expr1 ]
|
x7 [ var1 , var2 ]
|
x|
3](beke_paper25x.png)
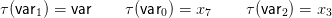
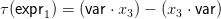

![expr0
|
[ var , expr ]
0 | 1
|
x7 [ var1 , var2 ]
| |
x x
5 3](beke_paper29x.png)