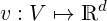
Vector representations of words were at the periphery of computer linguistics for decades however, recently they became widely used and researched.
In our terminology, representing a word consist of a function which assigns a vector (in ℝ d) to every word from a finite set (vocabulary) V .
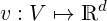
The first results concentrated on language modeling with neural architectures ([Xu and Rudnicky, 2000] and [Bengio et al., 2003]) instead of n-gram models ([Kneser and Ney, 1995]).
Referred as distributional vector semantics or word embeddings or word vectors, they are now off-the-shelf tools in NLP as of [Mikolov et al., 2013a] and [Pennington et al., 2014]. In these tools, the function v is learned from a corpus of unilingual, unlabeled, tokenized text. Their learning objective is similar to language modeling in the sense that they maximize the presence of a word in its neighboring context.
Word vectors are proven to be useful in applications: e.g. sentiment analysis [Socher et al., 2013], diachronic semantics change [W. Hamilton, 2016] or zero-shot learning [Dinu et al., 2015] and neural dependency parsing [Dozat et al., 2017] and scientifically investigated like [Arora et al., 2016].
In this paper we investigate certain properties and limitations of word vectors with the aim of improving them. We also present a novel method for learning not vector, but matrix representation of words.
In section 2 and 3 we lay out some theoretical backgrounds. Section 4 presents the actual training objectives and models. There are a few numerical results in section 5
As seen in [Mikolov et al., 2013c] and in [Mikolov et al., 2013b] the linear structure of a trained vector model is undeniable, meaning that the semantic structure is well represented by vector operations (linear combination and dot product). From analogy questions (king-man+woman=queen) through word similarity (angle of word vectors) and translation (vdog ⋅Teng to ger = vHund) to even some phrases (Chinese+river=Yangtze), the linear vector space structure seems to be empirically justified.
However, word vectors alone are not suitable for composing phrases or sequences of words. In the example above Chinese+river is not the same as "Chinese river", at least not more than "river Chinese". The vector addition is commutative, namely, one cannot distinguish the interchange of the components. This is why the vector addition itself is not suited for modeling composition. The sum of its words may represent a phrase but tackling the compositionality, in general, is a demanding task.
In [Socher et al., 2013] a parse tree was used to recursively process the phrases and make them into one sentence representation. In [Hill et al., 2016] an LSTM architecture (Long Short-Term Memory [Hochreiter and Schmidhuber, 1997]) was used to represent a phrase.
Learning compositional mechanisms and embeddings of various length entities (words, phrases and sentences) are in the central interest of novel neural language processing.
Naturally, the question arises; what are the appropriate mathematical structures (and composition rules) for a word embedding. The performance of the vector models suggest that the vector space structure is a good starting point. We also mentioned that beside the useful + operation, the words tend to have an additional operation, which composes them and this composition is non-commutative. An algebra over the real field is a reasonable choice [Rudolph and Giesbrecht, 2010].
In Figure 1 the symbols C, V , R and A represent commutative groups, vector spaces, rings and algebras respectively. A commutative group has a commutative addition operator (among others); in addition to that, a vector space has dot product (and also scalar multiplication). A ring has addition and (non-commutative) multiplication and an algebra is equipped with all of these operations.
Note that in a group, in theory, one can compute elements like Chinese+river or even subtract: Volga - Russia, but there is no way of comparing the result to existing vocabulary entries. In a vector space, the dot product can measure similarities between elements and the scalar multiplication gives us the ability to calculate averages over certain elements. In a ring, one can use the multiplication operator to model composition, but still lacks some aspects of the vector space. In an algebra, all of these requirements are met.
As a special case of algebras, matrix algebras consist square matrices and they are in the target of our studies. Hence the name matrix embedding: we want to train square matrices for each word in a vocabulary, given a corpus of sentences.
The algebra operations would look something like this:
| green + orange | ≈ yellow-ish color or a team with these colors | ||
| green * orange | ≈ "green orange" like an unriped fruit |
Let V be our vocabulary: a finite set of symbols (words). Let C ⊂ V * be a collection of sentences, i.e. corpus. We
seek a map which gives a matrix for each word: M : V  ℝd×d. The size of the matrices (d) is a model
parameter.
ℝd×d. The size of the matrices (d) is a model
parameter.
In order to train such a map, one has to impose an objective function which measures how good a sentence is.
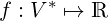
We wish to find an appropriate f and optimize it with respect to M given the corpus of sentences.
First of all, we make some restrictions of the function f. Since we want to model the composition via matrix multiplication, f will be evaluated solely on matrices, not on series of matrices. The score of a sentence should be the score of the product of its words.
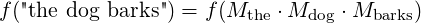
Note that the compositionality takes place in the matrix product, the product of three matrices is also a matrix, which is in the same vector space as its components, although not necessarily in the vocabulary.
As in [Pennington et al., 2014], we choose the score function to be linear in the components. In the example above, it is linear in all of its inputs: "the", "dog" and "barks".
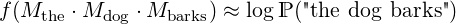
In our work we choose f similarly to [Rudolph and Giesbrecht, 2010]:
| f(M) | = v⊤⋅ M ⋅ w | ||
| f(Mthe ⋅ Mdog ⋅ Mbarks) | = v⊤⋅ M the ⋅ Mdog ⋅ Mbarks ⋅ w | ||
where v and w are column vector, depending on the model which will be specified later.
In the following subsections we introduce various models, which implement the above ideas. All of them are suitable for optimization and indeed train the embedding M but with different approaches. We detail the numerical results in section 5.
In the following model one does not assert a probability to a full sentence, but only a probability that a word fits in a context. f shall be such that

In formulas, the objective is to minimize the entropy in every context, like:
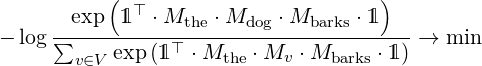
Or more precisely maximize the following in M.
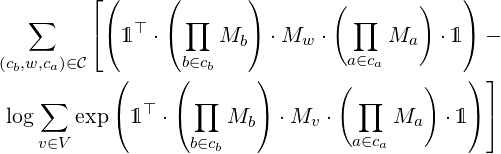
Note that this model does not assign probabilities to a whole sentence, only to certain choices of words. The probability of a sentence is hard to measure (see [Kornai, 2010]), therefore we do not require the model to calculate them.
One can rewrite the above model in a way that every sentence, phrase and word gets a directly calculated probability. As a motivation, we will try to eliminate the softmax in the neural model, which will lead us to the full probabilistic model.
If the softmax is to be eliminated, then the matrices Mw should be restricted to ensure the total probability of 1. A constraint will be added to M such that
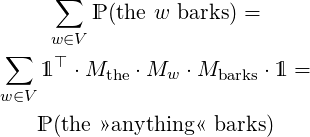
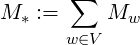
which does not change the probability of any sequence, no matter where it is inserted. And we also want thatℙ (»anything«) = 1.
In this model the matrices have an inevitable probabilistic interpretation. We postulate the following constraints over M:

i.e. its rows sum up to 1.
Under these conditions on can state the followings.
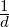 ⋅1⊤⋅
⋅1⊤⋅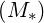 n ⋅1 = 1 for n = 0,1,2…
n ⋅1 = 1 for n = 0,1,2…
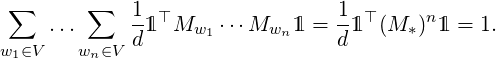
In this setup one can simply calculate the probability of any phrase or series of words as
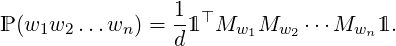
This model can be trained on a weighted corpus, where every sentence has an empirical probability p. In such a case, one has to minimize the KL divergence.
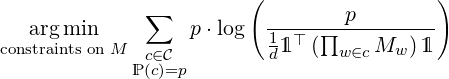
If the corpus has no weights then we assume p ≡ 1.
The models so far were discriminative models.
One can generalize wighted finite state automata by modifying the above model, and one can optimize a continuous finite state automaton to fit a weighted language. Similar connection between WFSAs and matrix representation of words can be found in [Asaadi and Rudolph, 2016]. We also introduce a learning algorithm to obtain our matrix embeddings, which in turn can help learning automata. As future work, these techniques may be relevant in MDL (Minimum Description Length) learning of automata, as in [Kornai et al., 2013].
One can see in the previous model that the left-hand-side of the product can be considered as a context or state vector.
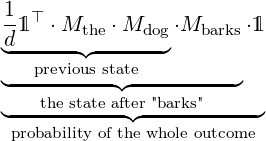
In a way, the initial row vector 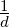 1⊤ is carried through the sentence and one can ask the probability of the current state
by applying the column vector 1.
1⊤ is carried through the sentence and one can ask the probability of the current state
by applying the column vector 1.
Some modification is needed to justify this intuition and introduce a WFSA. We change the constraints on the
embedding M, since the state of an automaton should always sum up to 1. In the previous model the sum of the earlier
mentioned row vector decreases as the sentence spans. Let Mw be a right-stochastic matrix for every word w ∈ V . In
this way the automaton starts from the uniform state 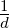 1⊤ and every word acts as a transition on this
state.
1⊤ and every word acts as a transition on this
state.
 | (1) |
Some additional action is required, since the sum of every state is now 1 and we want to obtain meaningful probabilities. Let R ∈ℝd×|V | be a matrix of non-negative entries which is responsible for the emissions. In neural network terminology we would call that readout layer.
At every state v the columns of the matrix R determine which word should follow.
 | (2) |
Constraints on R and M are listed below.
Under these constraints an automaton arises:
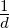 1⊤
1⊤
And the probability of an emission sequence is the following product
| ℙ(w1w2…wn) = | 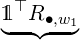 ℙ ℙ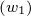 ⋅ ⋅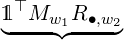 ℙ ℙ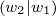  | ||
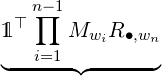 ℙ ℙ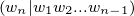 |
Given a corpus or a weighted language, one can use the same objective function as in the previous section and train M and R.
Note that, unlike in the previous two models, this model is not sensitive to the future words to come. The next emission and state does not depend on the following words. In contrast to the previous one, this is a generative model.
Our experimental setup used the UMBC gigaword corpus ([Han et al., 2013]) which was tokenized and split at sentence boundaries (punctuation part-of-speech tag). The words were not converted into lowercase. It contains about 3.338G words, the average length of a sentence is about 24 with standard deviation 15. For computational reasons, we excluded long sentences leaving 126.7M sentences to work with.
Words with frequency less than 52 were replaced with a unique symbol <UNK>, leaving roughly 100k types in the vocabulary (precisely 100147).
The implementation is not detailed herein, but the code is available1 .
We encountered some serious numerical obstacles in case of model 4.1. It is not certain that the numerical issues are the result of implementation or come from the mathematical model, but the problem occurs if the stochastic gradient descent encounters the same token repeated several times in the same sentence. Although, this problem did not occur neither in model 4.2 nor 4.3. The first model differs from the others in many aspects: implementation language, mathematical model, and also in gradient descent strategy.
Only the results of the second model are presented. The third model did not reach a reasonable quality within a reasonable computational time . The quality of the models were measured on Google Analogy questions [Mikolov et al., 2013a], see evaluation code below2 . Cosine similarity was used on the flattened matrices.
In table 1 one can read the number of correctly answered questions of each trained model. Commutative means that the matrices were 100 × 100 diagonal matrices, they form a commutative algebra. This can be considered as a fallback to word vectors. The dense models consist of 10 × 10 dense matrices.
The model 4.3 could answer 1 or 2 questions after the same amount of training.
We introduced several techniques to train matrix embeddings of words with various numerical efficiency and quality.
Training high quality embeddings and/or automata is our future interest. There are some obvious obstacles in computation time, since the training of a well tuned embedding usually takes a day and matrix models are expected to require more computations.
A possible computational enhancement is the use of structured, sparse matrices, where we train only certain elements in the matrices, hence taking a sub-algebra of the full matrix algebra. This hastens some calculations but keeps the desired algebra properties intact. To this end, further studies of matrix algebras and their sub-algebras are considered.
Currently these experiments are in a preliminary state but many improvements and applications are possible. As my supervisor once has described it:
“Like socialism; appealing idea, but not working in practice.”
— András Kornai
[Arora et al., 2016] Arora, S., Li, Y., Liang, Y., Ma, T., and Risteski, A. (2016). Rand-walk: A latent variable model approach to word embeddings. Transactions of the Association for Computational Linguistics (TACL), 4:385–399.
[Asaadi and Rudolph, 2016] Asaadi, S. and Rudolph, S. (2016). On the correspondence between compositional matrix-space models of language and weighted automata. In Proceedings of the ACL Workshop on Statistical Natural Language Processing and Weighted Automata (StatFSM 2016), Berlin, Germany.
[Bengio et al., 2003] Bengio, Y., Ducharme, R., Vincent, P., and Janvin, C. (2003). A neural probabilistic language model. Journal of Machine Learning Research, 3:1137–1155.
[Dinu et al., 2015] Dinu, G., Lazaridou, A., and Baroni, M. (2015). Improving zero-shot learning by mitigating the hubness problem. In ICLR 2015, Workshop Track.
[Dozat et al., 2017] Dozat, T., Qi, P., and Manning, C. D. (2017). Stanford’s graph-based neural dependency parser at the conll 2017 shared task. In Proceedings of the CoNLL 2017 Shared Task: Multilingual Parsing from Raw Text to Universal Dependencies, pages 20–30, Vancouver, Canada. Association for Computational Linguistics.
[Han et al., 2013] Han, L., L. Kashyap, A., Finin, T., Mayfield, J., and Weese, J. (2013). UMBC_EBIQUITY-CORE: Semantic textual similarity systems. In Second Joint Conference on Lexical and Computational Semantics (*SEM), pages 44–52, Atlanta, Georgia, USA. Association for Computational Linguistics.
[Hill et al., 2016] Hill, F., Cho, K., Korhonen, A., and Bengio, Y. (2016). Learning to understand phrases by embedding the dictionary. Transactions of the Association for Computational Linguistics, 4:17–30.
[Hochreiter and Schmidhuber, 1997] Hochreiter, S. and Schmidhuber, J. (1997). Long short-term memory. Neural Computation, 9(8):1735–1780.
[Kneser and Ney, 1995] Kneser, R. and Ney, H. (1995). Improved backing-off for m-gram language modeling. In International Conference on Acoustics, Speech, and Signal Processing, 1995. ICASSP-95., volume 1, pages 181–184. IEEE.
[Kornai, 2010] Kornai, A. (2010). Rekurzívak-e a természetes nyelvek? Magyar Tudomány, 171(8):994–1005.
[Kornai et al., 2013] Kornai, A., Zséder, A., and Recski, G. (2013). Structure learning in weighted languages. In Proceedings of the 13th Meeting on the Mathematics of Language (MoL 13), pages 72–82, Sofia, Bulgaria. Association for Computational Linguistics.
[Mikolov et al., 2013a] Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013a). Efficient estimation of word representations in vector space. In Bengio, Y. and LeCun, Y., editors, Proceedings of the ICLR 2013.
[Mikolov et al., 2013b] Mikolov, T., Le, Q. V., and Sutskever, I. (2013b). Exploiting similarities among languages for machine translation. Xiv preprint arXiv:1309.4168.
[Mikolov et al., 2013c] Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and Dean, J. (2013c). Distributed representations of words and phrases and their compositionality. In Burges, C., Bottou, L., Welling, M., Ghahramani, Z., and Weinberger, K., editors, Advances in Neural Information Processing Systems 26, pages 3111–3119. Curran Associates, Inc.
[Pennington et al., 2014] Pennington, J., Socher, R., and Manning, C. (2014). Glove: Global vectors for word representation. In Conference on Empirical Methods in Natural Language Processing (EMNLP 2014).
[Rudolph and Giesbrecht, 2010] Rudolph, S. and Giesbrecht, E. (2010). Compositional matrix-space models of language. In Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics, pages 907–916, Uppsala, Sweden.
[Socher et al., 2013] Socher, R., Bauer, J., Manning, C. D., and Andrew Y., N. (2013). Parsing with compositional vector grammars. In Proceedings of the 51st Annual Meeting of the Association for Computational Linguistics (ACL 2013), pages 455–465, Sofia, Bulgaria. Association for Computational Linguistics.
[W. Hamilton, 2016] W. Hamilton, J. Leskovec, D. J. (2016). Diachronic word embeddings reveal statistical laws of semantic change. ACL.
[Xu and Rudnicky, 2000] Xu, W. and Rudnicky, A. I. (2000). Can artificial neural networks learn language models? In International Conference on Statistical Language Processing, pages 202–205, Beijing, China.