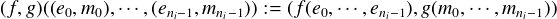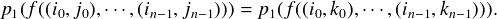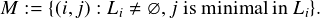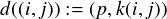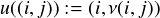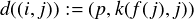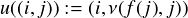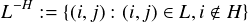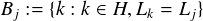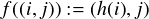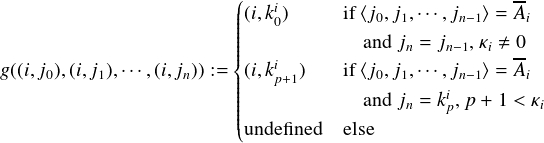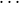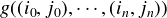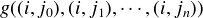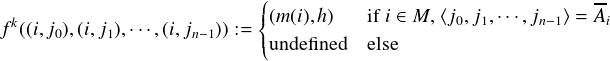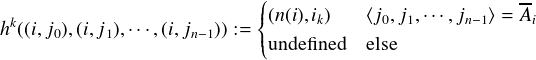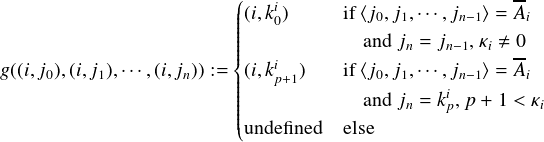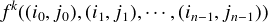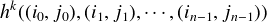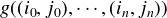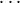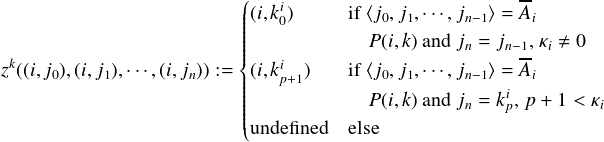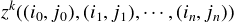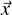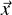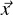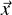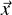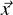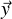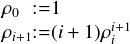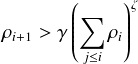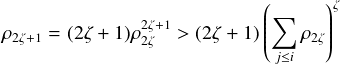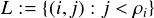Independently generated languages
Marcus Kracht1 & Tomasz Kowalski2
1Fakultät Linguistik und Literaturwissenschaften
Universität Bielefeld
2Department of Mathematics and Statistics
La Trobe University, Melbourne
1 Compositionality versus Independence
How do humans understand the meaning of a complex sentence they have never heard
before? The answer is that there is an algorithm that allows to compute the meaning of the
complex expression from its parts. While this much seems uncontroversial, semanticists have
actually argued that natural languages possess a stronger property, that of compositionality. A
language is said to be compositional if the meaning of a complex expression is a function of
the meaning of its parts given the mode of composition; thus, a language is compositional if
the algorithm computing the meaning can do so without knowing the expressions that
carry these meanings. It is this latter property that has been made into a litmus
test for formal semantic theories. A theory that provides a compositional account
of meaning is preferred over one that does not. But how much of a constraint is
compositionality on a language? In other words, what empirical significance does it have
to say that a language is compositional? Do noncompositional languages at all
exist?
While the introduction of the subject is often credited to Montague, it is perhaps the work
that has been done in the wake of Montague that had put compositionality firmly on the
agenda of formal semantic theorising, see Janssen (1997) for an account by one of the
protagonists. The survey books Barker and Jacobson (2007) and Hinzen et al. (2012)
document the persistent interest in this notion. From a mathematical point of view, the
question is how much of an empirical content this notion has. Janssen has actually shown that
any language is compositional, provided no constraints on syntactic operations are being
made (see Janssen (1997)). Though his notion of language is slightly nonstandard, the result
holds also for languages in the Saussurean sense, ie relations between expressions and
meanings.
However, as Kracht (2011) has pointed out, the dual property, namely that the form of an
expression is independent of the meaning of its parts, is actually a well known hypothesis of
generative grammar: It is called the autonomy of syntax. It is curious that to our knowlede no
definition of this notion with the same explicitness has ever been given in print. In retrospect
it seems that a grammar that satisfies both of them simultaneously is really what linguistics
have been after, and not compositionality alone. We call this property independence. It has a
rather simple mathematical formulation, so the investigation may also be of interest in
combinatorial theory.
Moreover, it turns out that the property of independence is actually rather tricky. It is
still unclear whether there exists a countable language that is not independently
generated. Though we believe that such a language exists, we have not been able to
find one. The results here exhibit some positive results (specifying languages that
are independently generated) and reduces the complexity of the original problem
somewhat.
We thank our reviewer for suggesting ways to improve this paper. Also, Marcus Kracht
wishes to thank András Kornai for his friendship and the endless discussions on mathematics,
language and life.
2 Autonomy and Compositionality
A language is an arbitrary subset L of E × M, where E and M are given sets of expressions
and meanings, respectively. An independent grammar for L is a finite set F ⊆ L and
a finite set P of pairs of functions (fi,gi), i < m, such that for i < m there is an
ni (the arity of the functions) such that fi : Eni E and gi : Mni
E and gi : Mni M are both
partial functions and L is exactly the set that can be generated from F using P.
The action of such a pair is defined as usual: (f,g)((e0,m0),
M are both
partial functions and L is exactly the set that can be generated from F using P.
The action of such a pair is defined as usual: (f,g)((e0,m0),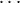 , (eni-1,mni-1)) is
defined if and only if both f (e0,
, (eni-1,mni-1)) is
defined if and only if both f (e0,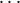 ,eni-1) and g(m0,
,eni-1) and g(m0,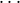 ,eni-1) are defined and in that
case
,eni-1) are defined and in that
case
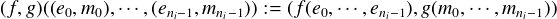
There is an obvious mathematical generalisation. Let R ⊆ ωd be a relation. Say that R is
independently generated if there is a finite set of partial functions fik, k < d, of arity ni (only
dependending on i) such that the product functions (fi0,fi1,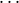 ,fid-1) (of arity ni) generate R
from a finite subset. The limiting case of d = 1 is trivial. Any countable subset of ω can be
generated; it suffices to pick one constant and a single unary function. Thus, the case
d = 2 is the first really interesting case. Notice also that if there is a relation of
arity d that is not independently generated, then there is an example in any higher
arity.
,fid-1) (of arity ni) generate R
from a finite subset. The limiting case of d = 1 is trivial. Any countable subset of ω can be
generated; it suffices to pick one constant and a single unary function. Thus, the case
d = 2 is the first really interesting case. Notice also that if there is a relation of
arity d that is not independently generated, then there is an example in any higher
arity.
Notation. If f is a function and S a set, put f [S] := {f (x) : x ∈ S}. Given L ⊆ ω2 we
write Li for the “column” {j : (i,j) ∈ L}. It follows that L = ⋃
i∈ω{i}× Li. Dually we write
jL := {i ∈ ω : (i,j) ∈ L}.
The notion of independence is restrictive. Let L ⊆ E ×M be countably infinite. Then there
exists a finite subset F and a finite number of partial functions on E × M (rather than
independent functions on E and M) generating L. Indeed, one constant plus a single unary
function is enough. Simply enumerate L = {(ei,mi) : i ∈ ω}, put F := {(e0,m0)} and let
f : E × M → E × M be defined by
 By
assumption, i is unique in the first case. Then it is easily seen that (ek,mk) = fk((e0,m0)), so
we generate exactly L.
By
assumption, i is unique in the first case. Then it is easily seen that (ek,mk) = fk((e0,m0)), so
we generate exactly L.
However, the question was whether it is possible to define the functions in such a way that
the actions on E and on M are independent of each other. In the linguistic literature, two
weaker notions have been discussed. The most important one is compositionality. The first
result will be that all countable languages have a compositional grammar.
Since the set of generating functions is finite, L is at most countably infinite. Thus we can
restrict E and M to some countably infinite subset; without loss of generality we
can assume them to be the set of natural numbers ω = {0, 1, 2, 3,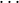 }. (Formally,
there is nothing that distinguishes members of E from members of M.) Thus, from
now on E = M = ω. Let p1 : ω2 → ω : (i,j)
}. (Formally,
there is nothing that distinguishes members of E from members of M.) Thus, from
now on E = M = ω. Let p1 : ω2 → ω : (i,j)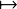 i and p2 : ω2 → ω : (i,j)
i and p2 : ω2 → ω : (i,j)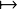 j.
j.
Definition 1 Let f be a partial n-ary function on ω2. We say that f is independent
in the first component if for all pairs (i0,j0),  , (in-1,jn-1) and all pairs (i0,k0),
, (in-1,jn-1) and all pairs (i0,k0), 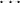 ,
(in-1,kn-1): f ((i0,j0),
,
(in-1,kn-1): f ((i0,j0),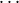 , (in-1,jn-1)) is defined if and only if f ((i0,k0),
, (in-1,jn-1)) is defined if and only if f ((i0,k0),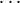 , (in-1,kn-1))
is defined, and if any of them is defined, then the first projection of the values are
identical, ie
, (in-1,kn-1))
is defined, and if any of them is defined, then the first projection of the values are
identical, ie
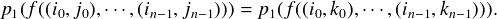 Dually the notion of independence in the second component is defined.
Dually the notion of independence in the second component is defined.
Theorem 2 Let L ⊆ ω2. Then there is a finite set of functions generating L from a
finite subset where all functions are independent in the first component. Likewise, the
is a finite set of functions generating L from a finite subset where all functions are
independent in the second component.
Proof. Obviously, we need to prove only the first claim. The second follows analogously. (Or
instead, apply the method to L⌣ := {(j,i) : (i,j) ∈ L} and then “switch” the solution.) Now,
consider first the language
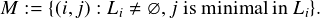 Clearly, M ⊆ L.
Clearly, M ⊆ L.
So M has the form M = {(i,ni) : i ∈ H} for some H ⊆ ω. Let α be the least member of H,
ie the least number such that Lα ⇔ ∅. Introduce a constant for (α,nα). Next, let k(i,j) be
defined as follows. In case j = ni and there is a q > i such that Lq ⇔ ∅, let k(i,j) := (p,np),
where p is the smallest number > i such that Lp is nonempty. If no such number exists, or if
j ⇔ ni, put k(i,j) := (i,j). Now put
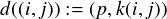 This defines our first function. (A) d is independent in the first component since p
can be established from i alone. (B) L is closed under d. For given (i,j) ∈ L, if
d((i,j)) = (i,j) then obviously d((i,j)) ∈ L. If d((i,j)) ⇔ (i,j), then (i,j) = (i,ni) and
d((i,j)) therefore has the form (p,np), where by definition (p,np) ∈ M. (C) M is the
closure of {(α,nα)} under d. We prove by induction on i that all (i,ni) ∈ M can be
generated. For i = α this is the case by assumption. Let i be given with (i,ni) ∈ M. Then
let p < i be the largest number such that (p,np) ∈ M. By inductive hypothesis,
(p,np) is generated from {(α,nα)}. But (i,ni) = d((p,np)), so it is also generated from
{(α,nα)}.
This defines our first function. (A) d is independent in the first component since p
can be established from i alone. (B) L is closed under d. For given (i,j) ∈ L, if
d((i,j)) = (i,j) then obviously d((i,j)) ∈ L. If d((i,j)) ⇔ (i,j), then (i,j) = (i,ni) and
d((i,j)) therefore has the form (p,np), where by definition (p,np) ∈ M. (C) M is the
closure of {(α,nα)} under d. We prove by induction on i that all (i,ni) ∈ M can be
generated. For i = α this is the case by assumption. Let i be given with (i,ni) ∈ M. Then
let p < i be the largest number such that (p,np) ∈ M. By inductive hypothesis,
(p,np) is generated from {(α,nα)}. But (i,ni) = d((p,np)), so it is also generated from
{(α,nα)}.
Next, define a function ν as follows. Given i and j, ν(i,j) := j if either j ℜ Li or j is the
largest member of Li. Otherwise, ν(i,j) yields the least j′ such that j′ ∈ Li and j′ > j. Now
put
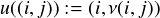 (A)
u is evidently independent in the first component. (B) L is closed under u. For if
(i,j) ∈ L and u((i,j)) = (i,j) then u((i,j)) ∈ L. Otherwise, u((i,j)) = (i,ν(i,j)) = (i,j′),
where among other j′ ∈ Li. So, u((i,j)) ∈ Li ⊆ L. (C) L is generated from M using
u. This is proved by induction on j. Choose (i,j) ∈ L. If j is minimal in Li then
j = ni and the claim trivially follows. Otherwise, choose j′ to be maximal such
that (i,j′) ∈ L and j′ < j. By inductive hypothesis, (i,j′) is generated from M
using u. But u((i,j′)) = (i,j), and so (i,j) is likewise generated from M using u.
□
(A)
u is evidently independent in the first component. (B) L is closed under u. For if
(i,j) ∈ L and u((i,j)) = (i,j) then u((i,j)) ∈ L. Otherwise, u((i,j)) = (i,ν(i,j)) = (i,j′),
where among other j′ ∈ Li. So, u((i,j)) ∈ Li ⊆ L. (C) L is generated from M using
u. This is proved by induction on j. Choose (i,j) ∈ L. If j is minimal in Li then
j = ni and the claim trivially follows. Otherwise, choose j′ to be maximal such
that (i,j′) ∈ L and j′ < j. By inductive hypothesis, (i,j′) is generated from M
using u. But u((i,j′)) = (i,j), and so (i,j) is likewise generated from M using u.
□
Notice that we have been able to define total functions. Consider a system F of generating
(partial) functions on E × M. This system is called compositional if each member f ∈ F is
independent in the second component; it is called autonomous if each member f ∈ F is
independent in its first component. We can rephrase the previous theorem as follows. A
language is compositional (autonomous) if it has a finite compositional (autonomous) set of
generating functions.
Corollary 3 Let L be a countable language.
- L is autonomous.
- L is compositional.
□
Here is a surprising consequence.
Corollary 4 Suppose that L is either many-to-one (=unambiguous) or L is
one-to-many. Then L is independently generated.
Proof. Consider the second case, ie assume that L is one-to-many (the other case being dual). Let
f : M → E be such that f (j) is the unique i such that (i,j) ∈ L. Define the grammar as in the
proof of Theorem 2. Now put
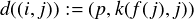 as
well as
as
well as
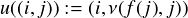 where k and ν are defined as before. By assumption, i = f (j), so that this defines the same
function. The so-defined functions do not depend on the first component any more, and so are
independent. □
where k and ν are defined as before. By assumption, i = f (j), so that this defines the same
function. The so-defined functions do not depend on the first component any more, and so are
independent. □
Corollary 5 Let L ⊆ E×M a language such that for some A ⊆ E, B ⊆ M, L∩A×B is
a many-to-one or one-to-many relation on A×B containing an infinite partial bijection.
Then L is independently generated.
Proof. We generate L ∩ A × B by means of independent partial functions defined on A × B, as
shown in Corollary 4. L contains a partial infinite bijection {(ai,bi) : i < ω}. Let
L-A×B = {(ei,mi) : i < ω}. Now add a new unary partial function f : A×B → (E-A) × (M -B)
with
 By
assumption, i is uniquely determined by x alone and by y alone, so f is actually independent.
□
By
assumption, i is uniquely determined by x alone and by y alone, so f is actually independent.
□
The notion of independence for languages is not the conjunction of autonomy and
compositionality (if it were, all languages would be independent, by Corollary 3); indeed, it
is much stronger than that. For it says that the language has an independent grammar, that is,
a grammar where every function is independent in both components. This is what we are
going to study now.
3 Basic Results
In using partial functions, here is a trick that will be used on several occasions.
Denote by [F]P the closure of F under P. Let A be the disjoint union of B and
C. Let P be a set of partial functions on B, and Q a set of partial function on C.
Take B0 ⊆ B and C0 ⊆ C. Then [B0 ∪ C0]P∪Q = [B0]P ∪ [C0]Q. To see that notice
that functions from P are undefined on every tuple containing elements from C,
and functions from Q are undefined on every tuple containing an element from B.
Therefore, functions from P cannot act on outputs of functions from Q, and vice
versa.
Lemma 6 Let L ⊆ ω2, and ω = E′∪ E′′, with E′ and E′′ disjoint, and let M ⊆ ω.
Now put L′ := L∩E′×M, L′′ := L∩E′′×M. Then if both L′ and L′′ are independently
generated, so is L ∩ ω × M.
Indeed, simply take the (disjoint) union of the constants and functions. The following two
claims are obvious.
Lemma 7 If L is independently generated, so is L⌣ := {(j,i) : (i,j) ∈ L}.
Lemma 8 Let π,ρ : ω → ω be injections. Let (π,ρ)[L] := {(π(e),ρ(m)) : (e,m) ∈ L}.
Then (π,ρ)[L] is independently generated iff L is independently generated.
There is a special corollary of this theorem that is worth stating separately. Consider the
case where Li = ∅ for certain i. Denote by U := {i : Li ⇔ ∅}. If U is infinite there is a
bijection ν : U → ω. Consider the language L∙ := (ν, idM)[L]. We have (L∙)i = Lν(i) ⇔ ∅ for
all i ∈ ω.
Corollary 9 L∙ is independently generated iff L is.
If U is finite, L is independently generated anyway, by the next theorem.
Lemma 10 Let n be a finite number.
- Every finite language is independently generated.
- n × n is independently generated.
- ω × ω is independently generated.
- ω × n, n × ω are independently generated.
- Every cofinite subset of ω × ω is independently generated.
Proof. The first claim is easy. Just introduce a constant for every element of L. The
second claim follows immediately. To show the third claim introduce a constant for (0, 0), and
two unary functions: one sending (i,j) to (i + 1,j), and one sending (i,j) to (i,j + 1). The
fourth claim is proved thus. For each j < n take a constant for (0,j). Finally, add a single
unary function sending (i,j) to (i + 1,j). For the last claim, let L = ω × ω -{(ik,jk) : k < n}.
Put E0 := {ik : k < n}, E1 := ω - E0; M0 := {jk : j < n}, M1 := ω - M0. Now L ∩ E0 × M0 is
finite; L ∩ E0 × M1 = E0 × M1, L ∩ E1 × M0 = E1 × M0, and L ∩ E1 × M1 = E1 × M1. The
first is independently generated since it is finite. The others are independently generated
because they are a simple product of at most countable sets. Now use Lemma 6.
□
Say that L is essentially bounded if L ⊆ n × ω or L ⊆ ω × n.
Lemma 11 Every essentially bounded language is independently generated.
Proof. >From Lemma 10 by repeated application of Lemma 6. □
Next we are going to reduce of the problem even further. Let H ⊆ ω such that for every
i ∈ H there is a j ℜ H and Lj = Li. Then put
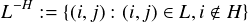
Lemma 12 If L-H is independently generated then L is independently generated.
Proof. Suppose that L-H is independently generated. For j ℜ H put
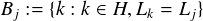 Now
let h : ω → ω be defined as follows. If j ℜ H and Bj = ∅ then h(j) := j. If j ℜ H and Bj ⇔ ∅,
then let h(j) := min Bj. Else, if j ∈ H then j ∈ Bi for some i. If j = max Bi, put h(j) := j,
otherwise let h(j) be the least j′ ∈ Bi such that j′ > j. Finally, let f be defined
by
Now
let h : ω → ω be defined as follows. If j ℜ H and Bj = ∅ then h(j) := j. If j ℜ H and Bj ⇔ ∅,
then let h(j) := min Bj. Else, if j ∈ H then j ∈ Bi for some i. If j = max Bi, put h(j) := j,
otherwise let h(j) be the least j′ ∈ Bi such that j′ > j. Finally, let f be defined
by
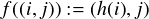 (A)
f is independent. (B) L is closed under f . Consider (i,j) ∈ L. If f ((i,j)) = (i,j) then
f ((i,j)) ∈ L. Otherwise, f ((i,j)) = (h(i),j), where by definition Lh(i) = Li. Thus,
(h(i),j) ∈ Lh(i) and so (h(i),j) ∈ L. (C) L is generated from L-H using f . If not, let i be
minimal such that for some j, (i,j) ∈ L but it is not generated from L-H using f . Then i ∈ H.
Let i′ the largest number such that i′ < i and i′ ∈ H if it exists, else let i′ ℜ H such that
i = min Bi′. By definition, i = h(i′). It is easily seen that (i′,j) is generated from L-H using f ;
the same is now true for (i,j). □
(A)
f is independent. (B) L is closed under f . Consider (i,j) ∈ L. If f ((i,j)) = (i,j) then
f ((i,j)) ∈ L. Otherwise, f ((i,j)) = (h(i),j), where by definition Lh(i) = Li. Thus,
(h(i),j) ∈ Lh(i) and so (h(i),j) ∈ L. (C) L is generated from L-H using f . If not, let i be
minimal such that for some j, (i,j) ∈ L but it is not generated from L-H using f . Then i ∈ H.
Let i′ the largest number such that i′ < i and i′ ∈ H if it exists, else let i′ ℜ H such that
i = min Bi′. By definition, i = h(i′). It is easily seen that (i′,j) is generated from L-H using f ;
the same is now true for (i,j). □
Thus we can restrict our search for nonindependent languages to those subsets of ω2
where all columns are different and all rows are different.
4 Main Theorems
We are going to investigate three conditions under which languages are independently
generated. The second and third conditions both generalise the first, in slightly different
directions. Examples will show that the generalisations are proper.
Definition 13 Let L ⊆ ω×ω. Say that L is n-discriminable if there is a family {Ai : i ∈ ω} of
sets such that:
- for each i: 0 < |Ai| ≤ n;
- for each i,j: if i ⇔ j then Ai ⇔ Aj;
- for every i: Ai ⊆ Li; and
- for every i,j Aj ⊆ Li if and only if j = i.
In that case, we call the family {Ai : i ∈ ω} an n-discriminating family for L. (Notice that 4.
implies 3.)
Notice that by definition, Ai ⊈ Aj for i ⇔ j. For if Ai ⊆ Aj we have Ai ⊆ Aj ⊆ Lj, from
which by definition i = j.
Theorem 14 Let L be n-discriminable. Then L is independently generated.
Proof. Let {Ai : i ∈ ω} be a discriminating family for L. Let Ai be a sequence of length n that
enumerates Ai, possibly repeating an element to reach length n. (Eg if n = 4 and A2 = {3, 6, 7}
then A2 = ⟨3, 6, 7, 7⟩ is a possible choice.) For each member of {(0,i) : i ∈ A0} we introduce a
constant. Now we define the following n-ary functions fk, k < n. Let h be the kth member of
Ai+1.
 | (1) |
Clearly this function is independent: on the first component it gives i + 1 if all arguments are
identical to i and is undefined otherwise. On the second component it gives h if the arguments
are exactly given as in Ai, and is undefined else. The partiality seems to be essential
here.
Now define a single n + 1-ary function g with the following action. For each i we assume
Li - Ai to be enumerated as {kji : j < κi} where κi < ω + 1 (so κi can be finite or
= ω).
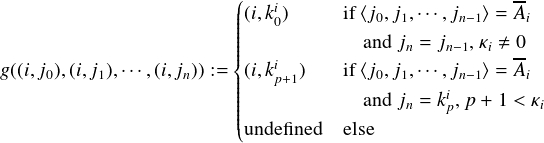 | (2) |
So defined g is independent. On the first coordinate the output is i if all inputs equal i; and is
undefined elsewhere. On the second coordinate it yields the next element in the enumeration
if there is one (and repeats the element if it is the last in the enumeration), provided the first n
arguments equal Ai; and is undefined elsewhere.
It now remains to be shown that this set of functions generates exactly L. There are two
parts: (i) the functions generate all of L; (ii) L is closed under the functions.
To prove (i), we shall first show that all {i}× Ai are generated using the fk and the
constants. Recall that all members of {0}× A0 are values of some constant. Now by
induction assume that {i}× Ai is generated. Thus all pairs (i,jp) exist, p < n, where
jp ∈ Ai. Then, using the functions fk, we can generate (i + 1,h), where h is the
kth member of Ai+1. Since all elements of Ai+1 appear at least once in Ai+1, all of
{i + 1}× Ai+1 is thus generated. Next we show that for every i, {i}× Li is generated
from {i}× Ai using the function g. To that end, recall that Li - Ai is enumerated as
k0i, k1i and so on for indices in κi. If κi = 0, nothing needs to be done. If κi > 0,
we get (i,k0i) as the value of g((i,j0), (i,j1), , (i,jn-1), (i,jn-1)), and (i,kp+1i)
as the value of g((i,j0), (i,j1),
, (i,jn-1), (i,jn-1)), and (i,kp+1i)
as the value of g((i,j0), (i,j1), , (i,jn-1), (i,kpi)). By induction, all values are
generated.
, (i,jn-1), (i,kpi)). By induction, all values are
generated.
Finally, we need to show that L is closed under the functions. Consider
 This
is defined only if i := i0 = i1 =
This
is defined only if i := i0 = i1 =  = in-1 and ⟨j0,j1,
= in-1 and ⟨j0,j1,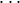 ,jn-1⟩ = Aq for some q. We have
q = i, since {i}× Ap ⊆ L only if p = i by definition of n-discrimination. So, the function is
defined only on fk((i,j0), (i,j1),
,jn-1⟩ = Aq for some q. We have
q = i, since {i}× Ap ⊆ L only if p = i by definition of n-discrimination. So, the function is
defined only on fk((i,j0), (i,j1),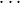 , (i,jn-1)), where ⟨j0,
, (i,jn-1)), where ⟨j0,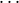 ,jn-1⟩ = Ai, and yields the value
(i + 1,j′k), where j′k is the kth member of Ai+1. By definition, this is in L. Next,
consider
,jn-1⟩ = Ai, and yields the value
(i + 1,j′k), where j′k is the kth member of Ai+1. By definition, this is in L. Next,
consider
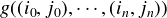 This
is defined only if i := i0 = i1 =
This
is defined only if i := i0 = i1 = 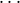 = in. Additionally, like in the case of fk, the sequence
⟨j0,j1,
= in. Additionally, like in the case of fk, the sequence
⟨j0,j1,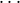 ,jn-1⟩ must equal Ai. Hence we have to look at
,jn-1⟩ must equal Ai. Hence we have to look at
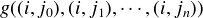 Several cases arise. (a) jn = jn-1. In that case we get (i,k0i), provided that κi > 0. In that case,
Li - Ai is nonempty, and contains k0i by definition. (b) jn = kpi, where kpi is a member of
Li - Ai. In fact, it is the pth member of the enumeration. If p + 1 = κi, then Li - Ai is
exhausted, and g is undefined. If not, we get (i,kp+1i), which is in Li - Ai by definition. (c)
The function is undefined on all other inputs. In all cases, we get values in L. The proof is
complete. □
Several cases arise. (a) jn = jn-1. In that case we get (i,k0i), provided that κi > 0. In that case,
Li - Ai is nonempty, and contains k0i by definition. (b) jn = kpi, where kpi is a member of
Li - Ai. In fact, it is the pth member of the enumeration. If p + 1 = κi, then Li - Ai is
exhausted, and g is undefined. If not, we get (i,kp+1i), which is in Li - Ai by definition. (c)
The function is undefined on all other inputs. In all cases, we get values in L. The proof is
complete. □
Corollary 15 Suppose that there exists an n such that for all i ∈ ω |Li| ≤ n. Then L is
independently generated.
Proof. By Lemma 12 we can reduce this to the case where for i ⇔ j Li ⇔ Lj. Define
I(j) := {i : |Li| = j} and Lj := ∪i∈I(j)Li. By Lemma 6, we need to show only that each of the
Lj is independently generated. To this end, it is enough to show that {Lij : i ∈ I(j)} is a
j-discriminating family. This is easy to verify. □
As an application, consider the language L = {(i,i), (i,i2) : i ∈ ω}. Here we can simply
take Ai := Li. Indeed, this is a 2-discriminating family. For |Ai| ≤ 2, the sets are nonempty,
pairwise distinct ({i,i2} = {j,j2} iff i = j), and, finally, if {i,i2} ⊆ Lj then j = i; for if
{i,i2} = {j,j2} then either the sets contain both two members, and then since i < i2,
j < j2 we have i = j; or they contain one member and then have the form {i} = {j},
from which again i = j. So, by the previous result the language is independently
generated.
A more complex example, to which this result cannot be applied, though, is
{(i,ik) : i,k ∈ ω}. It is a consequence of the next theorem that this language is independently
generated.
Definition 16 Call a language weakly n-discriminable if there is a family {Ai : i ∈ ω} of sets
such that
- for every i, 0 < |Ai| ≤ n;
- for every i,j: if i ⇔ j then Ai ⇔ Aj; and
- for every i, Ai ⊆ Li; and
- for every i,j: if Aj ⊆ Li then Li ⊆ Lj. (This is trivially true if i = j.)
In particular, if Ai ⊆ Aj then we must have Lj ⊆ Li. Clearly, all n-discriminable languages
are also weakly n-discriminable, but the converse does not hold, as the example just given
shows. For if L is n-discriminable, we must have Li ⊈ Lj for all i ⇔ j. (For if i ⇔ j and
Li ⊆ Lj, then since Ai ⊆ Li we also have Ai ⊆ Lj, which is excluded.) But the language
{(i,ik) : i,k ∈ ω} fails this: we have L2 ⊆ L4. On the other hand, the family defined by
Ai := {i,i2} is a weakly discriminating family. For if Ai ⊆ Lj then i = jp for some p, whence
Li = {ik : k ∈ ω} ⊆ {jp : p ∈ ω}. The next theorem establishes that this language is
independently generated.
Theorem 17 Let L be weakly n-discriminable. Then L is independently generated.
Proof. Let M := {i : for no j < i: Aj = Ai}. Furthermore, let B(i) = {j : Ai = Aj}. Thus, M
consists of all minimal members of the sets B(i). Now let m and n be unary partial functions
with the following action. m(j) is undefined if j is maximal in M, and otherwise it
is m(j) := min{k : k ∈ M,j < k}. n(j) is undefined if j is maximal in B(j), and
n(j) := min{k : k ∈ B(j),k > j} otherwise.
We need three sets of functions in addition to constants for the members of {0}× A0. The
first contains the functions fk, k < n. Define the sequences Ai as above, with the exception
that we require Ai = Aj if B(i) = B(j) (that is, if Ai = Aj).
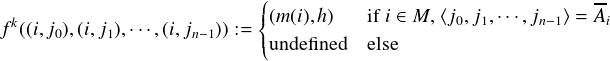 | (3) |
The second set consists of the hk, k < n.
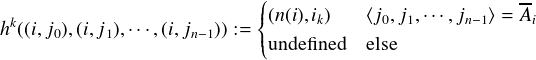 | (4) |
Finally, we define the function g as above:
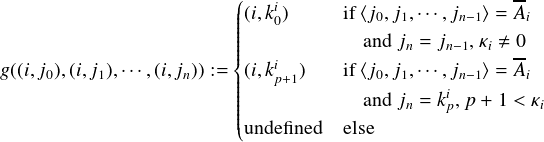 | (5) |
These functions are independent.
Again, we need to show that (i) L is generated from the functions, and (ii) L is closed
under these functions. As for (i), we note that by definition, we can generate all Ai where
i ∈ M from {0}× A0. Next, we can generate the {j}× Aj for all j ∈ B(j) just by applying the
hk, since we have generated its minimal members. Third, by using g we generate the columns
Li.
Now we show that L is also closed under the functions. Consider
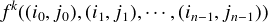 This
is defined only if i := i0 = i1 =
This
is defined only if i := i0 = i1 =  = in-1 ∈ M and ⟨j0,j1,
= in-1 ∈ M and ⟨j0,j1,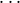 ,jn-1⟩ = Aq for some q. By
definition of M, for two numbers p,q ∈ M, Ap ⇔ Aq, and so q = i. The value (m(i),h) is in
Am(i) by definition of fk. Next consider
,jn-1⟩ = Aq for some q. By
definition of M, for two numbers p,q ∈ M, Ap ⇔ Aq, and so q = i. The value (m(i),h) is in
Am(i) by definition of fk. Next consider
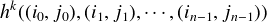 This
is defined only if i := i0 = i1 =
This
is defined only if i := i0 = i1 = 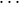 = in-1, and ⟨j0,j1,
= in-1, and ⟨j0,j1,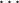 ,jn-1⟩ = Aq for some q. The value is
(n(i),jk); while jk is again in Aq, the new index is n(i). However, by choice of the function n,
An(i) = Ai, so we get a value from An(q). Thus, these functions are only defined on ⋃
q{q}×Aq
and yield values in that set.
,jn-1⟩ = Aq for some q. The value is
(n(i),jk); while jk is again in Aq, the new index is n(i). However, by choice of the function n,
An(i) = Ai, so we get a value from An(q). Thus, these functions are only defined on ⋃
q{q}×Aq
and yield values in that set.
Finally, we need to show that L is closed under g. Consider
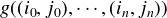 This
is defined only if i := i0 = i1 =
This
is defined only if i := i0 = i1 = 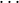 = in and ⟨j0,
= in and ⟨j0,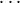 ,jn-1⟩ = Aq for some q. Now, suppose that
Aq = {j0,
,jn-1⟩ = Aq for some q. Now, suppose that
Aq = {j0,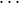 ,jn-1} ⊆ Li. Then by assumption on weak discriminability, Lq ⊆ Li. Hence, two
cases arise. (i) q = i. Then by definition of g, the value is in Li. (ii) p ⇔ i. Then, since the
value is in Lq, and Lq ⊆ Li, it is also in Li. □
,jn-1} ⊆ Li. Then by assumption on weak discriminability, Lq ⊆ Li. Hence, two
cases arise. (i) q = i. Then by definition of g, the value is in Li. (ii) p ⇔ i. Then, since the
value is in Lq, and Lq ⊆ Li, it is also in Li. □
Definition 18 Call L boundedly discriminable if there are numbers n and n′, an infinite set
M ⊆ ω and a family {Ai : i ∈ M} of sets such that the following holds:
- for each i ∈ M, |Ai| ≤ n;
- for each i ∈ M: Ai ⊆ Li;
- for each i ∈ M, the set B(i) := {j : Ai ⊆ Lj} has at most n′ elements; and
- for each i,j ∈ M, i ⇔ j, B(i) ∩ B(j) = ∅.
Every n-discriminable language is boundedly discriminable; just take M := ω. The sets
B(i) each have only one member in this case, so n′ := 1.
Actually, it follows that for each i,j ∈ M, i ⇔ j, Ai ⇔ Aj. For if i,j ∈ M and i ⇔ j, the last
clause implies j ℜ B(i), that is, Aj ⊈ Lj, so that Aj ⇔ Ai, since Ai ⊆ Li.
Notice that allowing M to be finite would not gain anything, as then the set of indices
would be finite, bounded by some multiple of |M|. So the only remaining interesting case is
where M is infinite. Moreover, we could assume n = n′ to simplify the definition.
Theorem 19 Suppose that L is boundedly discriminable. Then L is independently
generated.
Proof. Without loss of generality we may assume that all the i ∈ M are minimal in B(i); in
particular, the least element of B(0) is 0 ∈ M. If i ℜ M let j < i be the least element of B(i).
Then j ∈ M and we put Aj := Ai.
First we introduce constants for {0}×A0. Next we introduce functions fk and hk, k < n, as
in the previous proof. Finally, for k < n′, let zk be an n + 1-ary function, defined similar to g
above. Let P(i,k) be the statement: i is the kth number in B(i). As before, order the elements
of Li - Ai for each i ∈ ω, and align the elements of Ai in a sequence kji of length
n.
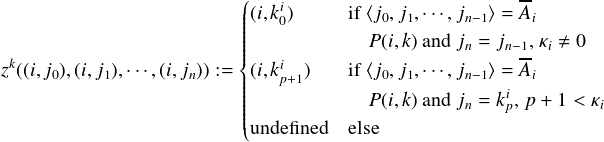 | (6) |
It remains that to show that (i) the functions generate L, (ii) L is closed under these functions.
(i) is reasonably clear. We generate Ai, i ∈ M, using the functions fk, and then all the
Ai using the gk as in the previous proof. Finally, the zk allow to generate all of Li
for P(i,k). Since for each number i there is a k < n′ such that P(i,k), we generate
Li from Ai using zk essentially as we used g. Now on to (ii). Closure under fk.
Consider
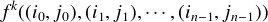 This
is defined only if i := i0 = i1 =
This
is defined only if i := i0 = i1 =  = in-1 ∈ M and ⟨j0,
= in-1 ∈ M and ⟨j0, ,jn-1⟩ ∈ Ai; and in that case it
yields the kth member of Aj, j the next member of M. Closure under hk. Pretty much as in the
previous proof. Closure under zk. Consider
,jn-1⟩ ∈ Ai; and in that case it
yields the kth member of Aj, j the next member of M. Closure under hk. Pretty much as in the
previous proof. Closure under zk. Consider
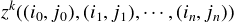 If
this is defined, i := i0 = i1 =
If
this is defined, i := i0 = i1 = 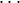 = in, i is the kth member of B(i), and Aq = ⟨j0,
= in, i is the kth member of B(i), and Aq = ⟨j0,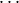 ,jn-1⟩ for
some q. If zk is defined, we know from q alone the identity of i. Thus, Li is known in
the second component. Now if Aq ⊆ Li, then q ∈ B(i) and so Aq = Ai. Now by
assumption either jn = jn-1, and we get the the least member of Li - Ai according to the
enumeration (if κi > 0). Or else we get the next member according to the enumeration.
□
,jn-1⟩ for
some q. If zk is defined, we know from q alone the identity of i. Thus, Li is known in
the second component. Now if Aq ⊆ Li, then q ∈ B(i) and so Aq = Ai. Now by
assumption either jn = jn-1, and we get the the least member of Li - Ai according to the
enumeration (if κi > 0). Or else we get the next member according to the enumeration.
□
5 Progressive Functions
The method has so far been to enumerate L by going through the Li in increasing order. The
interest in this method stems from using grammars to generate languages. We think of a
grammar as producing complex expressions from less complex expressions. In that sense, a
formation step produces a strictly more complex expression. Consider now an ordering of the
E of expressions in increasing complexity. Extend this to a linear order, and number the
expressions with natural numbers. We expect now that the meaning of expression j is
produced from some of the expressions 0, 1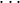 ,j - 1. This way of generating expressions is
called progressive.
,j - 1. This way of generating expressions is
called progressive.
We extend this now to functions on ω2 as follows. If f is an independent function on ω2 then it
has the form (f1(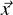 ),f2(
),f2(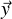 )). We say that f is (strictly, weakly) progressive if f1
is.
)). We say that f is (strictly, weakly) progressive if f1
is.
The functions in the previous proofs have generally been weakly progressive. The
following theorem shows why we cannot strengthen this to strongly progressive functions.
Theorem 21 There is a L ⊆ ω2 which cannot be generated by a finite strictly
progressive set of independent partial functions.
Proof. Suppose that F is a finite set of strictly progressive independent partial functions. Let γ be
the cardinality of F, and ζ the maximal arity of these functions. We may wlog assume that
γ = ζ. Then by progressivity, a member from Li is obtained by applying a function to the
members of ⋃
j<iLj. If their number is bounded by ki, then there are at most ζkiζ elements.
Thus, choose the following sequence of numbers.
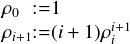 This
sequence is strictly increasing. Moreover, for each choice of γ and ζ there is i such
that
This
sequence is strictly increasing. Moreover, for each choice of γ and ζ there is i such
that
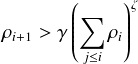 To
see this, note that ∑
j≤iρi ≤ iρi ≤ ρi2, since ρi > i (except for i = 0, 1, 2). Then
To
see this, note that ∑
j≤iρi ≤ iρi ≤ ρi2, since ρi > i (except for i = 0, 1, 2). Then
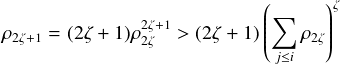 Now
define
Now
define
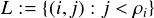 Then |Li| = ρi for all i. It follows that for i = 2ζ + 1 there are not enough functions to generate
the elements of L2ζ+1 for the elements with lower index. □
Then |Li| = ρi for all i. It follows that for i = 2ζ + 1 there are not enough functions to generate
the elements of L2ζ+1 for the elements with lower index. □
6 Conclusion
We have shown that all countable languages are compositional and autonomous. Moreover,
some results have been obtained concerning languages that are independently generated.
However, it is open whether all countable languages are independently generated. It is also
unclear whether or not allowing partial functions rather than total functions makes a
difference.
The conjecture is that there exist nonindependent countable languages. However, no
example has been found.
References
Barker, C. and P. Jacobson (Eds.) (2007). Direct Compositionality. Number 14 in
Oxford Studies in Theoretical Linguistics. Oxford: Oxford University Press.
Hinzen, W., E. Machery, and M. Werning (Eds.) (2012). Handbook of
Compositionality. Oxford University Press.
Hodges, W. (2001). Formal features of compositionality. Journal of Logic,
Language and Information 10, 7–28.
Janssen, T. (1997). Compositionality. In J. van Benthem and A. ter Meulen (Eds.),
Handbook of Logic and Language, pp. 417–473. Amsterdam: Elsevier.
Kracht, M. (2011). Interpreted Languages and Compositionality. Number 89 in
Studies in Linguistics and Philosophy. Springer.
Zadrozny, W. (1994). From Compositional Semantics to Systematic Semantics.
Linguistics and Philosophy 17, 329–342.
 E and gi : Mni
E and gi : Mni M are both
partial functions and L is exactly the set that can be generated from F using P.
The action of such a pair is defined as usual: (f,g)((e0,m0),
M are both
partial functions and L is exactly the set that can be generated from F using P.
The action of such a pair is defined as usual: (f,g)((e0,m0), , (eni-1,mni-1)) is
defined if and only if both f (e0,
, (eni-1,mni-1)) is
defined if and only if both f (e0, ,eni-1) and g(m0,
,eni-1) and g(m0, ,eni-1) are defined and in that
case
,eni-1) are defined and in that
case