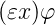
Key words and phrases. lambda calculus, epsilon symbol.
1.1. Hilbert’s epsilon, descriptions and FOL.
The first-order language (FOL) extended by the Hilbertian variable binding operator ε is possibly a good choice as an environment modelling a couple of formal linguistic and language philosophical phenomena concerning descriptions.1 The term
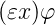 | (1) |
where φ is a FOL formula and x is a variable, has the following intuitive meaning:
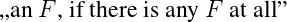 | (2) |
where predicate F is the intended meaning (or the natural language translation, if one likes it) of the formula φ. The intuition above comes straightforward from the first epsilon (or transfinite) axiom introduced by David Hilbert, which is the following formula scheme
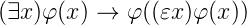
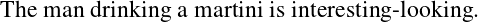 | (3) |
in FOL extended by ε (this extended language is denoted by FOL+ε).2 Since, FOL+ε does not contain definite descriptions, the phrase “the man drinking a martini” can be seen as a special case of the use of epsilon. A possible solution is to add a uniqueness clause to the formula ‘mandrinkingamartini(x)’ (the formula in FOL+ε expressing the natural language predicate “…is a man and drinks a martini”.)3
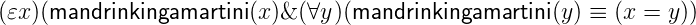
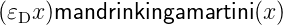 | (4) |
Then the sentence (3) is formulated as follows
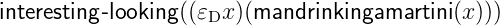 | (5) |
Let me remark again, the claim that the phrase “the man drinking a martini” can be expressed by
(εD x)mandrinkingamartini(x) is not an obvious one, however a possibly good enough working hypothesis.
Without a man holding martini in his hand, the meaning of “the man drinking a martini” is as vague as the
meaning of the phrase “the man drinking a martini, if anybody at all”.
Accepting the hypothesis above, one can formally analyse the act referring to the interesting-looking person in
question, even if he holds a glass of water in his hand. In this case, the reference of the term (4) is a person – not
drinking a martini – who seems to be interesting.
The problem of sentence (5) reminds one of Russell’s Theory of Descriptions (RTD). In Russell’s On Denoting
or in [Whit] it is proposed that descriptions must not to be considered as proper names, but incomplete parts of
quatified sentences.
Thus we must either provide a denotation in cases in which it is at first sight absent, or we must abandon the view that the denotation is what is concerned in propositions which contain denoting phrases. [Russ, p. 484]
According to the view I advocate, a denoting phrase is essentially part of a sentence, and does not, as like most single words, have any significance on its own account. [Russ, p. 488]
According to RTD descriptions, as denoting phases, are not interchangeable by identical ones, since they are meaningless in separation, but have only contextual meanings. Russell in the On Denoting gives a FOL reformulation for the sentences of the form (3),4 but in the general case, when the natural language sentence contains more than one descriptions or a lot of logical operators the FOL reformulation can be carried out several ways. One must mind the scope of logical operators and descriptions. Hence, in the general case RTD is rather a FOL reformulation program, in the spirit of the treatment of the simple case described in [Russ]. At this point, a bit naive question arises.
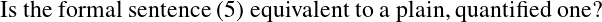 | (6) |
If it is in general, then RTD, or better say its quantificational program, is applicable to FOL+ε, in the sense that
the denoting phrases, containing the sentence, can be considered as incomplete parts of a quantified
reformulation.5
If it is not in general, then for FOL+ε Donnellan’s proposal holds (i.e. sometimes descriptions have referential meaning
too).6
The answer seems to be the latter. The term (εx)φ is a referring one (its semantic value is always defined)
and its semantic is unproblematic, even if there is no φ, at least the reference of (εx)φ is not a φ.
Nevertheless, be careful, RTD is a proposed strategy for the problem ‘how to deal with descriptions’
and not even a (mathematical) thesis. (εx)φ, in FOL+ε, is a proper name (in the sense meant by
Russell), hence the question must be rewritten in a weak form. But what will be this weakened
question?
It is well-known that if the truth value of the sentence ψ((εx)φ) in any model does
not depend on the semantic value of (εx)φ, then there is a FOL reformulation of
ψ((εx)φ).7
Hence, if ψ((εx)φ) is an epsilon-invariant formula (its semantic value is independent from the value of the
containing epsilon-term) then the term (εx)φ can be eliminated from ψ((εx)φ), up to logical equivalence. The
problem is that, this plain FOL reformulation is not an explicit or transparent one. The proof of the
theorem applies Craig’s Interpolation Theorem, which is a pure existence theorem not giving the
needed explicit formula. Hence, in the light of the above considerations, the relevant question is the
following.
Is there an explicit, transparent, well-explainable FOL reformulation of ψ((εx)φ), provided that ψ((εx)φ) is epsilon-invariant (in some model)?
For FOL+ε, the question has been positively answered in [Moln], however under a lot of technical conditions. When one changes FOL to lambda calculus the picture becomes much more clear. The point is that, in FOL the substitution ψ[x∕(εx)φ] is only a meta language operation, but in the lambda calculus it is encoded into the object language via the application MN, where N is supposed to be an epsilon-term of the form (εx)P .
1.2. Hilbert’s epsilon and the lambda operator.
In Section 2, it will be given a syntax and semantics for the epsilon symbol in the context
of typed lambda calculus (TL). The syntactic notions will be the well-known ones, but in the
definitions different way will be followed, based on the tree-technique in the spirit of Curry–Howard
Isomorphism.8
Since, by the Curry–Howard Correspondence, TL is closely related to the proof theory of the natural deduction
system of the propositional logic, a possibility is realised to define the TL syntax notions in the same
style as proofs. The form of the definitions will fit to this doctrine and a tree-based method will be
applied.
In Section 3, it will be seen that in TL the result can be reached much more faster
than in FOL. No need to refer to the so called intensional and substitutional epsilon
semantics.9
The strategy will be the following. The typed lambda language extended by Hilbert’s epsilon ( λ∀ε) will be
considered as a formal model of the fragment of the natural language containing descriptions. Then, if it is
possible, the epsilon expressions will be eliminated and the sentences containing them will be mapped, in an
explicit way, to the epsilon-free quantified reduct
λ∀ε) will be
considered as a formal model of the fragment of the natural language containing descriptions. Then, if it is
possible, the epsilon expressions will be eliminated and the sentences containing them will be mapped, in an
explicit way, to the epsilon-free quantified reduct  λ∀ of
λ∀ of  λ∀ε. The plain lambda language reformulation will
keep the logical truth in the model. Giving Montague semantics to the extended language and to the plain
epsilon-free language as models (the (𝔐,f)-s and the 𝔐-s below, respectively) the construction will be
unproblematic.
λ∀ε. The plain lambda language reformulation will
keep the logical truth in the model. Giving Montague semantics to the extended language and to the plain
epsilon-free language as models (the (𝔐,f)-s and the 𝔐-s below, respectively) the construction will be
unproblematic.
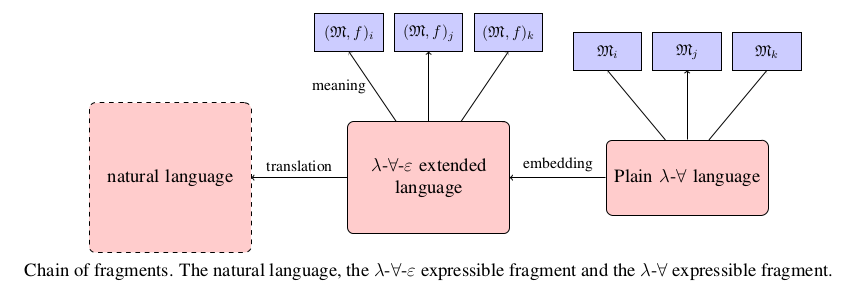
In Section 4, it will pointed out that the result is not less effective than the RTD proposed by Russell.
For the building of the syntax a tree-based method was chosen (parsing or construction trees),
which is much more transparent than the old fashioned character sequence technique. Mind that,
here the trees grow upward. Sorry for the inconvenience, if you are a mathematician expert of the
lambda calculus. Usually, upward growing trees are used by linguists in Combinatory Categorial
Grammar. And, what is the main motivation, such trees are used in the natural deduction style proof
theory.
The definitions below are basically combinations of the well-known ones from [Troe] Sec. 1. and
from the online lecture notes Sorensen, M. H. B., Urzyczyn, P., Curry–Howard Isomorphism
(1998)10 .
The so called typeability relation (⊢) is a pure syntactic relation which joins the expressions of the lambda
calculus to types with respect to a fixed set of typed variables called context. Of course, the relation ⊢ plays a
fundamental role in the Curry–Howard Isomorphism, which links the lambda expressions to proof trees of the
natural deduction system of the implicational logic.
Definition 1.The language of types is the tuple  Typ =
Typ = ![⟨ι,o,(,),[,]⟩](molnarz8x.png) . The set of its strings Srt(
. The set of its strings Srt( Typ) contains
the finite sequences of characters from {ι,o, (, ), [, ]}. A construction tree Π of the string γ ∈ Srt(
Typ) contains
the finite sequences of characters from {ι,o, (, ), [, ]}. A construction tree Π of the string γ ∈ Srt( Typ) is a
finite, labeled, ordered tree such that the labels of Π are from Srt(
Typ) is a
finite, labeled, ordered tree such that the labels of Π are from Srt( Typ) and
Typ) and
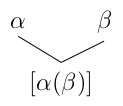
If there is a tree Π such that Π is a construction tree of α ∈ Srt( Typ), then α is said to be a type (expression) in
Typ), then α is said to be a type (expression) in
 Typ . The set of all types in
Typ . The set of all types in  Typ is denoted by Exp(
Typ is denoted by Exp( Typ). (Cf. [Troe, p. 9] Def. 1.2.1, [Troe, p. 7] Def.
1.1.7.)
Typ). (Cf. [Troe, p. 9] Def. 1.2.1, [Troe, p. 7] Def.
1.1.7.)
Note that the construction tree of a type is unique. The construction tree of the type α is denoted by Tree(α). The
referring to brackets [, ] is avoided when a type α is well-known and its construction tree can be completely
reconstruct without them.
Intuitively, ι is the type of individuals and o is the type of sentences. The compound type o(ι) is, for example, the
grammatical type of the single-variable predicates.
Definition 2.A lambda language is a tuple  λ =
λ = ![⟨V, C,(,),λ,[,]⟩](molnarz9x.png) , where V is an infinite and C is non-empty
set and V is disjoint to C. Srt(
, where V is an infinite and C is non-empty
set and V is disjoint to C. Srt( λ) contains the finite sequences from V ∪C ∪{λ, (, ), [, ]}. A construction tree Π
of the M ∈ Srt (
λ) contains the finite sequences from V ∪C ∪{λ, (, ), [, ]}. A construction tree Π
of the M ∈ Srt ( λ) is a finite, labeled, ordered tree such that the labels of Π are from Srt(
λ) is a finite, labeled, ordered tree such that the labels of Π are from Srt( λ)
and
λ)
and
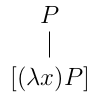
If there is a tree Π such that Π is a construction tree of M ∈ Srt( λ), then M is said to be an expression in
λ), then M is said to be an expression in  λ. The
set of all expression in
λ. The
set of all expression in  λ is denoted by Exp(
λ is denoted by Exp( λ).
λ).
The elements of V are called the variables of  λ and V is denoted by Var(
λ and V is denoted by Var( λ) and the members of C are
the constants of
λ) and the members of C are
the constants of  λ and C is denoted by Const(
λ and C is denoted by Const( λ). (Cf. [Troe, p. 9] Def. 1.2.2, [Troe, p. 7] Def.
1.1.7.)
λ). (Cf. [Troe, p. 9] Def. 1.2.2, [Troe, p. 7] Def.
1.1.7.)
Note that, the construction tree of an expression is unique. The construction tree of the expression M is
denoted by Tree (M). The height of Tree(M) is defined by the well-known manner and is denoted by
|Tree (M)|.
Referring to brackets [, ] is avoided, when an expression M is known and its construction tree can be completely
reconstruct without them.
Definition 3.Let ![⟨V,C, (,),λ,[,]⟩](molnarz10x.png) be a lambda language. The tuple
be a lambda language. The tuple  λ =
λ = ![⟨V, C,(,),λ,[,],Z⟩](molnarz11x.png) is a typed
lambda language, if Z : C → Exp(
is a typed
lambda language, if Z : C → Exp( Typ). The function Z is denoted by CnstTp(
Typ). The function Z is denoted by CnstTp( λ).
λ).
Definition 4.Let  λ be a lambda language and let Ξ ⊆ Var(
λ be a lambda language and let Ξ ⊆ Var( λ) be a non-empty finite set. A function
f : Ξ → Exp (
λ) be a non-empty finite set. A function
f : Ξ → Exp ( Typ) is called a context, and the set of all contexts are denoted by Cont(
Typ) is called a context, and the set of all contexts are denoted by Cont( λ).
(Ξ : Γ) ∈ Cont (
λ).
(Ξ : Γ) ∈ Cont ( λ) denotes a function f with domain Ξ and range Γ. If f = (Ξ : Γ) is a context, and
x ∈ Ξ then (x : γ) denotes f(x) = γ.
λ) denotes a function f with domain Ξ and range Γ. If f = (Ξ : Γ) is a context, and
x ∈ Ξ then (x : γ) denotes f(x) = γ.
For a typed lambda language  λ the sets of variables, expressions, contexts etc. defined and denoted by the
same manner as for a lambda languages.
λ the sets of variables, expressions, contexts etc. defined and denoted by the
same manner as for a lambda languages.
Definition 5.Let  λ be a typed lambda language. By induction on the height of the construction tree of
the expressions, relation
λ be a typed lambda language. By induction on the height of the construction tree of
the expressions, relation
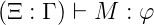
 λ), expression M ∈ Exp(
λ), expression M ∈ Exp( λ) and type φ. ⊢ is called
typeability relation.
λ) and type φ. ⊢ is called
typeability relation.
 λ) and (Ξ : Γ) is a context, then (Ξ : Γ) ⊢ c : φ, if φ = CnstTp(
λ) and (Ξ : Γ) is a context, then (Ξ : Γ) ⊢ c : φ, if φ = CnstTp( λ)(c).
λ)(c).
 λ) and (Ξ : Γ) is a context, then (Ξ : Γ) ⊢ x : φ, if (x : φ) ∈ (Ξ : Γ).
λ) and (Ξ : Γ) is a context, then (Ξ : Γ) ⊢ x : φ, if (x : φ) ∈ (Ξ : Γ).For some example, see [Troe, p. 10]
Definition 6.Let M≠∅. By induction on |Tree(φ)|, the domain set DM(φ) of the type φ ∈ Typ is defined as
follows.
Typ is defined as
follows.
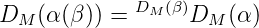
If M is fixed, then D(φ) is written instead.
Definition 7.If M≠∅,  λ is a lambda language and (Ξ : Γ) is a context, then a function a : Var(
λ is a lambda language and (Ξ : Γ) is a context, then a function a : Var( λ) →
∪φ∈
λ) →
∪φ∈ Typ DM (φ) is an assignation of the variables. The assignation a is an assignation of the type (Ξ : Γ),
if for every x ∈ Ξ, a(x) ∈ DM(α) whenever (x : α) ∈ (Ξ : Γ).
Typ DM (φ) is an assignation of the variables. The assignation a is an assignation of the type (Ξ : Γ),
if for every x ∈ Ξ, a(x) ∈ DM(α) whenever (x : α) ∈ (Ξ : Γ).
Definition 8.Let  λ be a typed lambda language, M≠∅. The tuple 𝔐 = ⟨M, Ip𝔐⟩ is a model over the
language
λ be a typed lambda language, M≠∅. The tuple 𝔐 = ⟨M, Ip𝔐⟩ is a model over the
language  λ , if Ip𝔐 : C →∪φ∈
λ , if Ip𝔐 : C →∪φ∈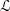 TypD(φ) such that Ip𝔐(c) ∈ D(CnstTp(
TypD(φ) such that Ip𝔐(c) ∈ D(CnstTp( λ)(c)).
λ)(c)).
Definition 9.Let  λ be a typed lambda language, 𝔐 = ⟨M, Ip𝔐⟩ a model over the language
λ be a typed lambda language, 𝔐 = ⟨M, Ip𝔐⟩ a model over the language  λ, (Ξ : Γ) a
context and a an assignation of the type (Ξ : Γ). Suppose, for N ∈ Exp(
λ, (Ξ : Γ) a
context and a an assignation of the type (Ξ : Γ). Suppose, for N ∈ Exp( λ) there is a type φ such that
(Ξ : Γ) ⊢ N : φ. By induction on |Tree(N)| the semantic value [[N]]a𝔐 in context (Ξ : Γ) is defined as
follows.
λ) there is a type φ such that
(Ξ : Γ) ⊢ N : φ. By induction on |Tree(N)| the semantic value [[N]]a𝔐 in context (Ξ : Γ) is defined as
follows.
 λ), then
λ), then
![𝔐 𝔐
[[c]]a = Ip (c).](molnarz14x.png)
 λ), then
λ), then
![𝔐
[[x]]a = a(x).](molnarz15x.png)
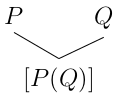
![[[P (Q )]]𝔐 = [[P]]𝔐([[Q ]]𝔐 ).
a a a](molnarz16x.png)
a[x → ξ](y) = a(y) for every variable y≠x, and a(x) = ξ.
Then
![[[(λx)P ]]𝔐 : D (α) → D (β );ξ ↦→ [[P]]𝔐
a a[x→ξ]](molnarz17x.png)
Note that, if N is not typeable in a context (Ξ : Γ), i.e. there is no type φ such that
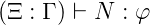
2.3. Logical and epsilon extensions.
The logical operators will be defined as constants of certain types. If  λ is a typed lambda language, then it
could be extended by the following constants.
λ is a typed lambda language, then it
could be extended by the following constants.
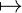 F,F
F,F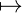 T in a model 𝔐,
T in a model 𝔐,
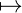 F, and T otherwise in a model 𝔐,
F, and T otherwise in a model 𝔐,
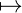 T)
T)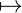 T, and F otherwise in a
model 𝔐,
T, and F otherwise in a
model 𝔐,
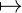 g({ξ ∈ M∣f(ξ) = T}),
g({ξ ∈ M∣f(ξ) = T}),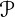 (M) → M such that g(S) ∈ S, if S≠∅ and g(S) ∈ M, if
S = ∅, in a model 𝔐.
(M) → M such that g(S) ∈ S, if S≠∅ and g(S) ∈ M, if
S = ∅, in a model 𝔐.In the following two specific extension will be mentioned, the plain extension
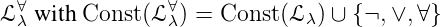
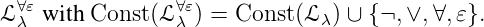
 λ ∀ , then (𝔐,g) will denote the (expanded) model of the
λ ∀ , then (𝔐,g) will denote the (expanded) model of the  λ∀ε extension with a choice function g described
above.12
λ∀ε extension with a choice function g described
above.12
), P &Q = ¬ (∨ ([¬ (P )](¬(Q )))), (∀x )P = ∀((λx )P)](molnarz27x.png)
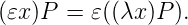
 λ∀ε= using identity of individuals is also introduced and the meaning of = is
defined as
λ∀ε= using identity of individuals is also introduced and the meaning of = is
defined as
 T, if x = y and F otherwise in a model 𝔐.
T, if x = y and F otherwise in a model 𝔐.
Proposition 1.Let x be a variable and (𝔐,g) be model over the language  λ∀ε=. Then
λ∀ε=. Then
Proof.(1)
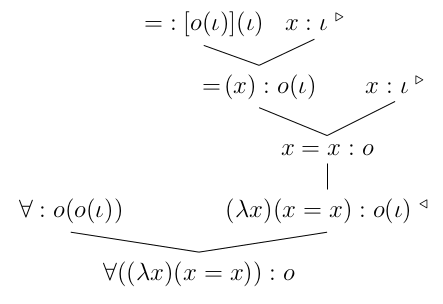
Here (= (x))(x) is denoted by x = x. The proof tree above shows that the expression ∀((λx)(x = x)), which is the
same as (∀x)(x = x), is typeabe by the type o. The labels ⊳ on the left sides of the leaves mark the places
which are called the “dischargeable premises” in proof theory. Their role is abandoned at the node
labeled by ⊲ . According to the part (2b) of Definition 5, both the x : ι-s are discharged by the node
(λx)([= (x)](x)) : o(ι), i.e. (x : ι) can be canceled from the context, which is now an empty set. Note that, the
use of the labels ⊲ and ⊳ are completely unnecessary, since the role of the variable x is exactly that of the
triangles. The variable x in the leaves marks the “dischargeable premises” and the symbol (λx)
marks the node discharging the premises labeled by the free variable x, and then x becomes a bound
variable.
(2)
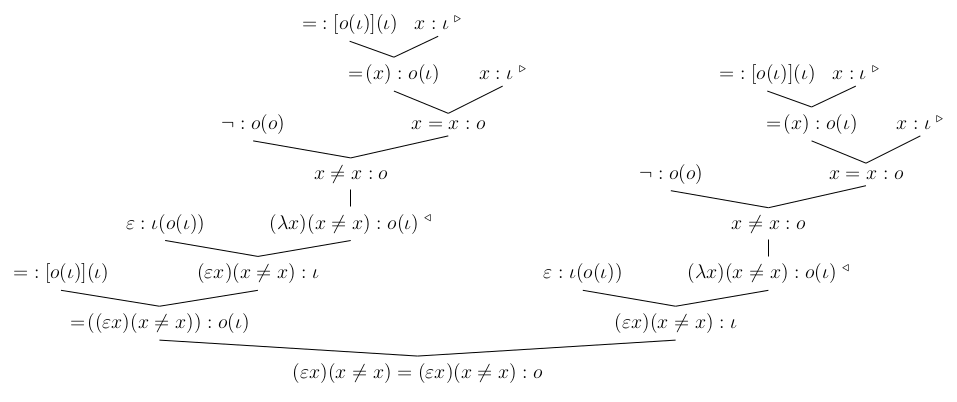
Here, according to definition, ε((λx)(x≠x)) is denoted by (εx)(x≠x) and ¬(x = x) is denoted by x≠x. The
above proof tree proves that (εx)(x≠x) = (εx)(x≠x) is typeable by o.
(3)
| [[(∀x)(x = x)]]a(𝔐,g) | = [[∀((λx)(x = x)]] a(𝔐,g) | ||
| = [[∀]]a(𝔐,g)([[(λx)(x = x)]](𝔐,g)) a | |||
= [[∀]]a(𝔐,g)(ξ [[= (x)(x)]]
a[x→ξ](𝔐,g)) [[= (x)(x)]]
a[x→ξ](𝔐,g)) | |||
= [[∀]]a(𝔐,g)(ξ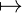 [[= (x)]]
a[x→ξ](𝔐,g)(ξ)) [[= (x)]]
a[x→ξ](𝔐,g)(ξ)) | |||
= [[∀]]a(𝔐,g)(ξ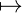 [[=]]
a[x→ξ](𝔐,g)(ξ)(ξ)) [[=]]
a[x→ξ](𝔐,g)(ξ)(ξ)) | |||
= [[∀]]a(𝔐,g)(ξ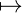 T) T) | |||
| = T |
The second expression’s semantic value is trivial:
| [[(εx)(x≠ x) = (εx)(x≠x)]]a(𝔐,g) | = [[=]] a(𝔐,g)([[(εx)(x≠x)]] a(𝔐,g))([[(εx)(x≠x)]] a(𝔐,g)) | ||
| = T |
however, it is worth to determine the epsilon term’s value:
| [[(εx)(x≠x)]]a(𝔐,g) | = [[ε((λx)(x≠x))]] a(𝔐,g) | ||
| = [[ε]]a(𝔐,g)([[(λx)(x≠x)]] a(𝔐,g)) | |||
= [[ε]]a(𝔐,g)(ξ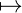 [[x≠x]]
a[x→ξ](𝔐,g)) [[x≠x]]
a[x→ξ](𝔐,g)) | |||
| = g({ξ ∈ M∣[[x≠x]]a[x→ξ](𝔐,g) = T}) = g(∅) | |||
| = g({ξ ∈ M∣[[¬]]a[x→ξ](𝔐,g)([[=]] a[x→ξ](𝔐,g)(ξ)(ξ)) = T}) = g(∅) | |||
2.5. Epsilon-invariant expressions.
Definition 10.Let N ∈ Exp( λ∀ε) be such that for a context (Ξ : Γ) the relation (Ξ : Γ) ⊢ N : φ holds
for a type φ and let 𝔐 be a
λ∀ε) be such that for a context (Ξ : Γ) the relation (Ξ : Γ) ⊢ N : φ holds
for a type φ and let 𝔐 be a  λ∀ model. N is said to be epsilon-invariant over the model 𝔐, if for every
assignation a of the type (Ξ : Γ) and choice functions g1,g2 :
λ∀ model. N is said to be epsilon-invariant over the model 𝔐, if for every
assignation a of the type (Ξ : Γ) and choice functions g1,g2 : 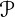 (M) → M it holds that
(M) → M it holds that
![(𝔐,g1) (𝔐,g2)
[[N ]]a = [[N ]]a .](molnarz35x.png)
The notion above is a symbolic formulation of the intuitive term “epsilon-independent”. In FOL this concept was applied to show that “epsilon-independent” sentences can be reformulated into an epsilon-free one, provided the sentence is independent over every model.13
Theorem 1.Let P,Q ∈ Exp( λ∀ε), 𝔐 be a model of
λ∀ε), 𝔐 be a model of  λ∀, (Ξ : Γ) a context, (Ξ : Γ) ⊢ P : o,
(Ξ : Γ) ⊢ Q : o and x ∈ Var(
λ∀, (Ξ : Γ) a context, (Ξ : Γ) ⊢ P : o,
(Ξ : Γ) ⊢ Q : o and x ∈ Var( λ∀ε), furthermore, let [(λx)P]((εx)Q), P and Q be epsilon-invariant over
the model 𝔐. Then for every assignation a of the type (Ξ : Γ) and choice function g :
λ∀ε), furthermore, let [(λx)P]((εx)Q), P and Q be epsilon-invariant over
the model 𝔐. Then for every assignation a of the type (Ξ : Γ) and choice function g : 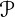 (M) → M:
(M) → M:
Q )]](𝔐a,g) = [[((∀x)(¬Q )& (∀x )P ) ∨ (((∃x )Q)& (∀x)(Q → P ))]](𝔐,g)](molnarz36x.png)
Proof.(1) Let the right hand side be T. First case: [[((∀x)(¬Q)&(∀x)P)]]a(𝔐,g) = T. Then [[(∀x)P )]]a (𝔐,g) = T holds and let m = [[(εx)Q]] a(𝔐,g) ∈ M. Hence, by definition
![(𝔐,g) (𝔐,g)
T = [[(∀x )P )]]a = [[∀((λx )P)]]a](molnarz37x.png)
![( (𝔐,g) )
[[(λx )P ]](𝔐a,g) = ξ ↦→ [[P ]]a[x→ξ] ≡ T.](molnarz38x.png)
Q )]](𝔐,g)= [[[(λx )P]]](𝔐,g)(m ) = [[P ]](𝔐,g) = T.
a a a[x→m ]](molnarz39x.png)
![(𝔐,g) ( (𝔐,g))
[[(λx )¬Q ]]a = ξ ↦→ [[¬Q ]]a[x→ ξ] ⁄≡ T](molnarz40x.png)
Q)]]a = [[[(λx )P ]((εx)Q )]]a = [[P ]]a[x→m ] = [[P ]]a[x→m ]](molnarz41x.png)
Q)]](a𝔐,g)= [[[(λx )P ]((εx)Q )]](a𝔐,g′)= [[P ]](𝔐,g) = [[P ]](𝔐,g)
a[x→m ] a[x→m ]](molnarz42x.png)
The concluding facts can be stated in two claims:
 λ∀ε (which is supposed to model the behaviour of descriptions) the
(closed) term (εx)Q has referential meaning in the sense that a fixed model (𝔐,g) points out an
individual [[(εx)Q]](𝔐,g) ∈ M for (εx)Q as semantic value.
λ∀ε (which is supposed to model the behaviour of descriptions) the
(closed) term (εx)Q has referential meaning in the sense that a fixed model (𝔐,g) points out an
individual [[(εx)Q]](𝔐,g) ∈ M for (εx)Q as semantic value.
 λ∀.
λ∀.We do not intend to set up a theory which is receiving fewer results than Russell’s Theory of Descriptions. A new theory must serve at least as many solutions as far as Russell’s proposal was able to solve. An appropriate indicator is to look at the two problems that the Theory of Descriptions solved and examine what the new model results in this field. The first one is the problem of Hesperus and Phosphorus (below, it will be called Morning Star Test), the second one is the problem of the empty names (the King of France Test).
In 1905, Russell gave a FOL based solution of the so called Frege Puzzle by RTD, understandably, without mentioning the intensional tools of possible world semantics, which is a much later development. Here, I would like to show briefly that even the exposition of the puzzle is so widely criticized, that the RTD result of the test is rather irrelevant to us.
“Gottlob thinks that the Morning Star is illuminated by the Sun.”
“The Evening Star is the Morning Star.”
—
“Gottlob thinks that the Evening Star is illuminated by the Sun”. (Cf. [Freg].)
First of all, I would like to point out that several scholars are committed to the standpoint that
the names such as “the Morning Star” or “the Evening Star” are understood tacitly as definite
descriptions. For Russell, these names abbreviate descriptions, hence they are denoting phrases
too.14
The problem is that, according to Leiniz’s Rule, since the Evening Star is the Morning Star, the two phrases
are interchangeable. However, the above inference does not seem to be valid, since it is possible
that Gottlob thinks that the Morning Star is illuminated by the Sun, but he does not necessarily
know this fact about the Evening Star, even if in reality the two planets are the same, which is the
case. Russell’s solution was that the phrases “the Morning Star” and “the Evening Star” are not
proper names, they only have contextual meanings, hence they are not interchangeable due to formal
reasons.15
In the epsilon language  λ∀ε, the definite descriptions are proper names, they are manifested as epsilon terms on
the object language level, hence the epsilon modelling fails the Morning Star Test, it does not explain the puzzle.
Fortunately, hitherto, the Frege Puzzle and the semantic status of the expressions like “the Morning star” are not
completely solved. If the phrase “the Morning star” is a rigid designator, what is Kripke’s proposal, then the
Puzzle is solved. Here, temporarily, not having modal context, ‘rigid’ means that the model points out
a single individual immediately, and does not select first a set, then a member of it, by a choice
function.16
Then the puzzle only says that, if planet Venus is illuminated by the Sun, then planet Venus is
illuminated by the Sun. According to Kripke’s solution the problematic one is the sentence
“The Evening Star is the Morning Star”. It is a necessary truth, but it may be epistemologically
problematic.17
For the epsilon model, the solution is the same. According to Monk the closed epsilon terms are constants,
therefore they are rigid designators in accordance with the Kripke doctrine. However, as Fitting pointed out, an
epsilon term, being description-like, can neither be a constant, nor a variable. It is a complex flexible
designator.18
Here, if “the Morning star” is a complex demonstrative (selected by a descriptive term in the actual world), then it is a rigid
designator.19
Clearly, now, I do not have to deal with the modal context of epsilon terms, knowing that the highly applicable
tool of demonstratives might make the modal approach much more complex, and might not add essentially more
to the above consideration.
λ∀ε, the definite descriptions are proper names, they are manifested as epsilon terms on
the object language level, hence the epsilon modelling fails the Morning Star Test, it does not explain the puzzle.
Fortunately, hitherto, the Frege Puzzle and the semantic status of the expressions like “the Morning star” are not
completely solved. If the phrase “the Morning star” is a rigid designator, what is Kripke’s proposal, then the
Puzzle is solved. Here, temporarily, not having modal context, ‘rigid’ means that the model points out
a single individual immediately, and does not select first a set, then a member of it, by a choice
function.16
Then the puzzle only says that, if planet Venus is illuminated by the Sun, then planet Venus is
illuminated by the Sun. According to Kripke’s solution the problematic one is the sentence
“The Evening Star is the Morning Star”. It is a necessary truth, but it may be epistemologically
problematic.17
For the epsilon model, the solution is the same. According to Monk the closed epsilon terms are constants,
therefore they are rigid designators in accordance with the Kripke doctrine. However, as Fitting pointed out, an
epsilon term, being description-like, can neither be a constant, nor a variable. It is a complex flexible
designator.18
Here, if “the Morning star” is a complex demonstrative (selected by a descriptive term in the actual world), then it is a rigid
designator.19
Clearly, now, I do not have to deal with the modal context of epsilon terms, knowing that the highly applicable
tool of demonstratives might make the modal approach much more complex, and might not add essentially more
to the above consideration.
Consider the following two sentences
“The present King of France is bald.”
“The present King of France is not bald.”
In order to determine the truth value of the first one, let us imagine the set of all bald people. Since the present
King of France is not in this set, the first sentence is false. But, the same reasoning leads to the
fact that the second sentence is false too. Which is a contradiction. Hence, the phrase “the present
King of France” is not a proper name, it cannot have a meaning in isolation, rather it only has a
contextual meaning and the sentences containing such phrases are quantified formulas. This is Russell’s
solution.
In the epsilon calculus the semantic values of the epsilon terms are defined in any cases. The two
sentences above are unproblematic, having the phrase “the present King of France” an existing
individual as reference. And it is either bald or not bald. According to Theorem 1 of the present
paper, the sentences may possess contextual meaning too, where the truth value is also well-defined.
Of course, the reference of “the present King of France” in the epsilon calculus is not the present
King of France. Approaching the situation on a more formal level, let us consider the symbolic
sentence
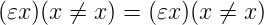
I would like to thank Endre Latabár, András Simon and the unknown reviewer for their helpful comments concerning specific parts of the paper or the whole one.
[Ahre] Ahrendt, W., Giese, M., Hilbert’s epsilon-Terms in Automated Theorem Proving, in Murray, N. V. (ed.), Automated Reasoning with Analytic Tableaux and Related Methods, International Conference, TABLEAUX ’99, (1999) pp. 171-185
[Blas] Blass, A. & Gurevich, Y., The Logic of Choice, The Journal of Symbolic Logic, Vol. 65, No. 3 (Sep., 2000), pp. 1264-1310 p
[Caic] Caicedo, Xavier, Hilbert’s ε symbol in the presence of generalized quantifiers In Quantifiers: Logics, Models, and Computation II Synthese Library, Vol. 249 (1995) p. 63-78.
[Donn] Donnellan, K., Reference and Definite Descriptions, Philosophical Review, vol. 75, (1966) pp. 281-304.
[Dumm] Dummett, M., Frege: Philosophy of Language. London, Duckworth (1973).
[Fitt] Fitting, M., An Epsilon-Calculus System for First Order S4, (1972) pp. 103-10 of W. Hodges (ed.). Conference m Mathematical Logic, 70, Springer.
[Freg] Frege, G., On Sense and Reference, (1892) in Translations from the Philosophical Writings of Gottlob Frege., trans. and ed. Geach, P. & Black, M., Oxford: Blackwell, 1952, 1960, pp. 56-78
[Hilb] Hilbert, D. & Bernays, P., Grundlagen der Mathematik, Vol. 2 (1939) Berlin, Springer.
[Kapl] Kaplan, D., Demonstratives, in Almog, J., Perry, J. and Wettstein, H., 1989. Themes from Kaplan, Oxford University Press., pp. 481-563.
[Knee] Kneebone, G. T., Mathematical Logic and the Foundation of Mathematics, Van Nostrand, London, (1963).
[Krip] Kripke, S., Naming and necessity, Harvard University Press, Cambridge, (1972).
[Mints] Mints, G., Thoralf Skolem and the Epsilon Substitution Method for Predicate Logic, Nordic Journal of Philosophical Logic, Vol. 1, No. 2, (1996) pp. 133-146.
[Moln] Molnár, Z., Epsilon-Invariant Substitutions and Indefinite Descriptions, Logic Journal of the IGPL, (2013) 21 (5), pp. 812-829.
[Monk] Monk, J. D., Mathematical Logic, Springer-Verlag, New York–Heidelberg–Berlin (1976)
[Russ] Russell, B., On Denoting, in: Mind, New Series, Vol. 14, No. 56 (Oct. 1905), pp. 479-493.
[Simm] Simmons, H., Derivation and Computation: Taking the Curry-Howard Correspondence Seriously, Cambridge Tracts in Theoretical Computer Science, Cambridge University Press; 1 edition (May 18, 2000).
[Slat07] Slater, H., Completing Russell’s Logic, Russell: the Journal of Bertrand Russell Studies, Vol. 27, Iss. 1 (2007), Article 15.
[Slat09] Slater, H., Hilbert’s Epsilon Calculus and its Successors, in: Handbook of the History of Logic, Logic from Russell to Church, Vol. 5 (2009), ed. Gabbay, D. M., Woods, J., North-Holland, pp. 385-448.
[Troe] Troelstra, A. S., Schwichtenberg, H., Basic Proof Theory, second edition. Cambridge: Cambridge University Press. (2000)
[Whit] Whitehead A. N., Russell, B., Incomplete symbols: Descriptions, (1910) in: From Frege to Gödel: a source book in mathematical logic 1879-1931, ed.: van Heijenoort, J., Harvard University Press (1967) pp. 216-223
[Zvol] Zvolenszky, Z., Searle on analicity, Necessity, and Proper Names, 2012, Organon F vol. 19, Supplementary Issue 2, pp. 109-136.
DEPARTMENT OF ALGEBRA, BUDAPEST UNIVERSITY OF TECHNOLOGY AND ECONOMICS, 1111 EGRY JóZSEF U. 1. BUILDING H, 5th flOOR, BUDAPEST, HUNGARY
E-mail address: mozow@math.bme.hu