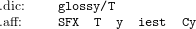
(1)
Giving birth to Finite State Phonology is classically attributed to Johnson (1972), and Kaplan and Kay (1994). However, there is an earlier discovery that was very close to this achievement. In 1965, Hennie presented a very general sufficient condition for regularity of Turing machines. Although this discovery happened chronologically before Generative Phonology (Chomsky and Halle, 1968), it is a mystery why its relevance has not been realized until recently (Yli-Jyrä, 2017). The antique work of Hennie provides enough generality to advance even today’s frontier of finite-state phonology. First, it lets us construct a finite-state transducer from any grammar implemented by a tightly bounded one-tape Turing machine. If the machine runs in o(n log n), the construction is possible, and this case is reasonably decidable. Second, it can be used to model the regularity in context-sensitive derivations. For example, the suffixation in hunspell dictionaries (Németh et al., 2004) corresponds to time-bounded two-way computations performed by a Hennie machine. Thirdly, it challenges us to look for new forgotten islands of regularity where Hennie’s condition does not necessarily hold.
Generative phonology (Chomsky and Halle, 1968) is a rule-based string rewriting system that has been scrutinized carefully over the years of its existence. One of the major weaknesses of the system is that it has been proven to be equivalent to Turing machines (TMs) (Chomsky, 1963; Johnson, 1972; Ristad, 1990). As the derivations of such a machine do not necessarily terminate, the system is seriously defective and impossible to falsify. Thus, an unrestricted rewriting allowed by Generative Phonology does not make a very good scientific theory in the light of Popper (1959), see also (Johnson 1972:32).
In spite of the original shortcomings and the increased depth in the current phonological theory, the original “SPE” formalism is interesting for its own sake. First, the formalism has been employed extensively in natural language processing and descriptive linguistics. There, it has been used to express phonological generalizations based on empirical data. Second, revisiting the original formalism and its decidable subsets can produce valuable ideas that are applicable to more ambitious theories, such as Optimality Theory (Prince and Smolensky, 2002) and Harmonic Serialism (McCarthy, 2000).
When realistic grammar instances in Generative Phonology have been studied closely, a striking contrast between the original undecidable theory and the actual grammars has been discovered. In pioneering studies (Johnson, 1972; Kaplan and Kay, 1994), most practical grammars in Generative Phonology have been shown to satisfy a two-part condition under which they correspond to finite-state transducers:
These observations have led to the development of algorithms for transforming restricted fragments, or islands, of Generative Grammar into finite-state transducers. For example, the algorithm of Mohri and Sproat (1996) constructs transducers from rules that are applied in a directed fashion. Karttunen (1995) treats various application modes and different types of context conditions. These finite-state islands in Generative Phonology have become standard textbook material (Jurafsky and Martin, 2000; Beesley and Karttunen, 2003) and many redesigned compilation algorithms have been proposed to pursue efficiency, flexibility and the generally correct semantics.
The literature of methods that compile individual rules into finite-state transducers suggests that regularity of phonological grammars is to be proven inductively, by using operations that preserve regularity of regular relations. But we should not overlook a more extensive picture of regularity as a property of the relation rather than as a property of the construction. Therefore, we should now start to pursue for a wider understanding of the archipelago of finite-state islands in generative theories as well as in all computational models of language.
Proving that the input-output relation defined by a grammar is regular is a complicated task. The known finite-state islands and the closure properties of finite-state transducers solve only the easy cases where the application order of rules is fixed and the rules can be combined under a finite composition. But if the grammar contains iterative rules, we do not have a general method that would return a non-iterative grammar. The regularity of the string relation defined by iterative rules is computationally undecidable already for context-free grammars (Stearns, 1967; Greibach, 1968), not to talk about Turing machines and equivalent grammars systems.
In light of this, we see that the fundamental results in Finite-State Phonology (Johnson, 1972; Kaplan and Kay, 1994) have given us only islands, sufficient conditions where the grammars or parts of grammars are finite-state and generate regular relations. They do not exclude new conditions that can also be valuable. New conditions are, ideally, constructive and turn a formerly nonconstructive property into a method that gives a finite-state transducer.
For example, it has been obvious since Chomsky and Halle (1968) that a phonological grammar is regular when it contains only right-linear (or left-linear) rules (Chomsky, 1963). The left-linear rules have the general shape α → βγ where α,β,γ are symbols and β does not match any left-hand side in the grammar rules. The achievement of Johnson (1972) was to expand the default regular subset of Generative Phonology by showing that the linear and the simultaneous application of phonological rules with context conditions can also generate a regular relation.
Kaplan and Kay (1994) also discuss general situations that are usually known as cyclic derivations (Mohanan, 1986). For example, the word unenforceable has the recursive structure [un[[en[force]]able]]. Here the phonological rules are applied first to the innermost part, force. Then the innermost brackets are removed and the application is repeated until no brackets are left. Kaplan and Kay point out that ”there may be restrictions on the mode of reapplication that limit the formal power of the [cyclic] grammar...”. However, Kaplan and Kay (1994:365) seem to think that these restrictions are analogous to context-free grammars with only right- or left-linear rules.
Besides context-free grammars with only right- or left-linear rules, there are also self-embedding grammars that generate regular languages. For example, the context free grammar S → aS∣Tb; T → Tb∣c generates the regular language a∗cb∗ and the context-sensitive grammar S → aS; aS → abT; bT → cbT∣c generates the regular language a∗c. In these examples, the grammars look simple but are not immediately regular on the basis of the shape of their rules.
In the sequel, Section 2 presents a concrete example of a very simple context-sensitive formalism whose conversion to a finite-state equivalent grammar is tricky. In Section 3, the reader is familiarized with a one-tape Turing machine and Hennie’s sufficient condition for regularity. The paper closes with remarks in Section 4.
We will now give an example of a grammar whose regularity is not obvious on the basis of the standard conditions.
Our example of a non-classical finite-state grammar is the hunspell formalism (Németh et al., 2004) that represents a stage in the development of spell checking algorithms. We only discuss its suffix rules and ignore many details of the formalism.
The hunspell formalism is used to inflect and derive word forms by a combination of continuation classes, truncation and appending. The formalism resembles the Item and Process morphology (Hockett, 1954) and Lexical Phonology (Mohanan, 1986). The formalism involves .dic and .aff files that specify the initial word forms and the steps to produce other word forms:
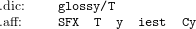 | (1) |
When the hunspell dictionary formalism is interpreted as a rewriting system, we see that the derivation glossyT ⇒ glossiest# is described with a Generative Phonological rule (2):
![Superlative-Formation:-
[y]T → [i][e][s][t][#] ∕ C-](yli-jyra1x.png) | (2) |
In order to analyse what actually happens, we need to construct a model that shows how the dictionary form is processed by the affix rules.
Now we analyse hunspell by viewing the derivation steps of its word formation as a process that corresponds to a computation by a particular TM.
The general definition of a Turing machine is assumed to be familiar to the reader. In short, it is a combination of a finite-state automaton and a rewritable two-way working tape that is initialized with the input string of length n. The machine is allowed to append new letters arbitrarily to the input string; thus the working tape is infinite. A TM can also have auxiliary tapes, but we will restrict ourselves to one-tape TMs.
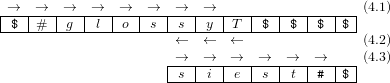
If we implement the derivation by the moves of a non-deterministic one-tape TM, we obtain a machine that sweeps the working tape three times in a row. During the first pass (3.1), the machines recognize the stem (glossy) and its continuation class (T), then rewinds the tape (3.2) to the beginning of the string and non-deterministically replaces the substring syT$$$ with the substring siest# during the final pass (3.3):
 | (3) |
Since regular relations are closed under composition, a finite number of similar suffix rules could be applied in a row and the lexicon would still be regular. In this way, k suffix positions of morphology could be treated. The corresponding non-deterministic TM would rewind the tape k times to the beginning. Thus, the total time complexity is in O(nk) when the string on the tape occupies at most n tape squares. Thus, the non-deterministic TM implementation of a finite composition has linear time complexity.
In a more general situation, one does not want to specify the maximum number of suffixes explicitly. One reason can be that, in some languages, the suffixes can be added recursively after one other. For example, a Turkish word can, in principle, have an arbitrary number of suffixes although only some of the combinations are interpretable. Another example involves Old Georgian where the nouns can theoretically have unlimited number of case-number markers (Michaelis and Kracht, 1997). Finally, orthographic compounding of many languages can involve several stems and alternating bound morphemes. For example, the Swedish word (with our morpheme boundaries) Spår-vagn-s-aktie-bolag-s-sken-smut-s-skjut-are-fack-förening-s-personal-beklädnad-s-magasin-s-förråd-s-förvaltar-en-s contains 14 stems and, in addition, several bound morphemes. Similar and much longer examples can be found in other languages. E.g. a 431-letter word appears in the Sanskrit literature. Thus, it is hard to argue that the number of rule applications has a finite upper bound in general.
The unbounded number of applications of suffix rules breaks the two principles: non-self-embedding rules and finite composition. Moreover, the implementation based on a rewinding TM would spend O(n2) time to produce the derived string through the back and forth sweeps that simulate the composition steps.
We can, however, improve the TM implementation by optimizing its moves. Instead of rewinding the tape completely, the improved computation strategy (4) just backs up until it has tested the precondition. In our example, the precondition is just the suffix [C][y][T]:
 | (4) |
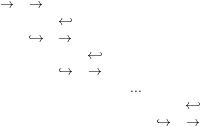 | (5) |
Since the union of the affix-rules is applied repeatedly to its own output, the standard two-part regularity condition of phonological grammars does not apply. However, as long as the derivation deletes and appends new material only at the right end of the string, the resulting process is linear and, intuitively, a regular grammar. In addition, the moves taken by the TM can now be deterministic because the machine does not completely rewind the tape at any point but always makes relative moves that allow it to remember its previous position.
Although the grammar represented by a hunspell lexicon does not satisfy the classical two-part condition of finite-state phonology, it is equivalent to a finite-state transducer when restricted to the suffix rules.
There are now some methods to compile hunspell lexicons to finite-state transducers. Early experiments on compilation are due to Gyorgy Gyepesi (p.c., 2007) and others in Budapest. The author developed his solution (Yli-Jyrä, 2009) using a variant of Two-Level Morphology (Koskenniemi, 1983). This method viewed the lexicon as a collection of constraints that described linearly encoded backing up and suffixation in derivations. The method included an efficient one-shot compilation algorithm to compile and intersect several hundreds of thousands of lexical context restriction rules in parallel as if the lexical continuations (morphotaxis) were phonological constraints. A similar method, finally implemented by his colleagues, Pirinen and Lindén (2010), separated the lexical continuations from the phonological changes at morpheme boundaries and used a three-step approach where the final step composed the lexicon with the phonology. A separate compiler for lexical continuations was used and a two-level grammar described the phonological realization of morphemes in different contexts.
The key to understanding the method of Yli-Jyrä (2009) is that the computations of the TM are encoded as a linear string (6.2). This string is produced if the derivation actually reaches the final continuation class # whereas infinite loops do not correspond to an output string.
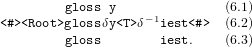 | (6) |
Whenever the machine overwrites its own output, the overwritten part (already on the left from the current position) is marked as deleted. The deleted material is put between <D> and <-D>, two symbols abbreviated now as δ and δ−1, respectively. The occurrence these optional lexical symbols is enforced in deleting contexts but banned otherwise, corresponding to the surface realizations with and without contractions. For example, the segment y in (6.2) is surrounded by a pair of δ and δ−1 because it is cancelled by -iest, the next hunspell affix.
The derivation of the combination of glossy and -iest is encoded as string (6.2). This internal string is then mapped to the output string (6.3) by a transducer that deletes the markers and the material enclosed between each pair of δ and δ−1. The computation can also be mapped to the dictionary form (6.1) by removing the markers and the material that belongs to the affixes.
An interesting part in the method is that the underlying derivation encodes a computation of a bounded Turing machine (6.2). This string is produced with context-restriction rules introduced in two-level phonology (Koskenniemi, 1983). Since the output deletions are taken care of by the simple transducer between (6.2) and (6.3), it is sufficient to describe only one representation level. The three rules in (7) describe where the root (Root) of the lexicon is visited, where a continuation class T is reached, and how the next (in fact final) continuation class is reached after a consonant, a cancelled y and new material corresponding to lexical -iest.
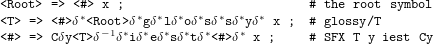 | (7) |
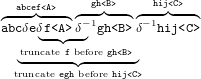 | (8) |
The main functional difference between the methods described by Yli-Jyrä and Pirinen and Lindén is in the way they treat non-disjoint deletions. While the former method encodes the sequence of derivation steps as one string, the latter encodes the lexical morpheme sequences on one string and then the contracted sequences in the other level. The latter method describes the contractions at morpheme boundaries via two-level rules that constrain the way in which the underlying phonemes of a morpheme are realized in the adjacency of various affixes. In this approach, a contraction corresponds to zero realization.
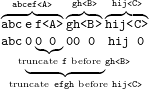 | (9) |
In particular, note that the addition of the suffix hij<C> in (8) and (9) requires different suffixation rules as the truncations behave differently. The rule applied in (9) must truncate more symbols. This semantic difference between the two methods can be compensated with an additional pre-processing step that expands the set of suffixation rules. During this step, a suffix rule that completely cancels the previous affix is replaced with a suffix rule that is applied before the completely cancelled affix. However, for most hunspell lexicons, the cancellation is restricted to the most recent suffix, which means that the preprocessing step can be heuristically ignored.
In the previous section, we related the hunspell derivations to one-tape TMs. One reason to do so was that the regularity of one-tape TMs is an old and carefully studied, well-understood problem.
In this section, we first relate one-tape Turing machines with transducers (§3.1-3.2). Then we study bounded one-tape TMs that implement regular relations (§3.3). We will use the bounded one-tape TMs to give a new proof for the two-part regularity condition (§3.4) and to find a more general condition for a finite-state subset of Generative Phonology (§3.5). Finally, we observe (§3.6) that even this condition does not cover all natural finite-state grammars.
Usually one-tape TMs and Hennie machines are viewed as language recognizers. Since it is not possible to construct a Hennie machine with two readable tapes Hennie (1965), the connection between Hennie machines and one-way two-tape finite-state transducers is not obvious from the beginning. In fact, most of the relevant literature discusses Hennie machines as if they were equivalent to one-tape finite-state automata only.
As a notable exception, Engelfriet and Hoogeboom (2001) connect Hennie machines to two-way two-tape finite-state machines. These machines are not allowed to read their output tape, but they are more powerful than ordinary finite-state transducers.
Our way to view one-tape Turing machines as transducers requires only the input tape with both reading and writing. As the machine modifies the contents of the input tape during its computations, the input tape will be occupied with an output string when the machine halts. Thus, every one-tape TM recognizes three sets:
Given the last definition, every one-tape TM can be viewed as a recognizer of a binary relation.
It is immediate that one-way finite-state transducers are equivalent to one-tape Turing machines: One-way (non)deterministic finite-state transducers are a special case of two-way (non)deterministic finite-state transducers and these are a special case of (non)deterministic two-tape Turing machines that are equivalent to deterministic one-tape Turing machines.
If we restrict ourselves to finite-state transducers whose output preserves the length of their input, we can view these transducers as one-tape finite automata with a letter-pair alphabet (Kaplan and Kay, 1994). This gives an even more direct link from finite-state transducers to one-tape Turing machines.
The restriction to these letter transducers is not a serious restriction if we assume that the necessary 0’s are introduced non-deterministically to the input string by an inverse homomorphic mapping h−1 : Σ∗→ (Σ ∪{0})∗ that preserves the alphabet Σ. The 0’s are then removed from the output string by the homomorphism h : (Σ ∪{0})∗→ Σ∗. In addition, we assume that all states of the transducer have a self-loop on the letter pair (0,0).
Let R1 and R2 be regular relations recognized by unrestricted finite-state transducers, and let R1′ and R2′ be the corresponding same-length relations recognized by the letter transducers with the self-loops. Now we have the equation:
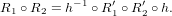
It is now obvious that same length relations R1′, R2′ and even R1′∘ R2′ can be implemented as non-deterministic one-tape TMs that recognize the relations in O(n) time by transforming the initial content of the tape to the final content of the same tape.
The most ground-breaking regularity condition for one-tape TMs is due to Hennie. Hennie’s result is the converse to the fact that every one-way deterministic finite automaton is a deterministic TM. The machines considered by Hennie do not only include all one-way deterministic finite automata and letter transducers but they also extend them in two particular ways: (1) the one-tape TMs can move back and forth on the tape, (2) they can overwrite on the squares of the tape several times.
Hennie (1965) showed that a deterministic one-tape TM is equivalent to a finite automaton if it runs in O(n). The result of Hennie have been extended, by Tadaki et al. (2010) to linear-time non-deterministic one-tape TMs whose o(n) time bound includes all accepting computations. A deterministic and non-deterministic linear-time one-tape TM are called a Hennie machine and a non-deterministic Hennie machine, respectively. Both of these one-tape machines recognize a regular relation on the basis of Section 3.1.
Hennie analysed the expressive power of one-tape machines using the concept of crossing sequence (aka schema) (Rabin, 1963; Trakhtenbrot, 1964; Hopcroft and Ullman, 1979; Birget, 1996) that is strongly related to visiting sequences (Fischer, 1969). This concept is a powerful tool in the analysis of the behaviour of two-way automata and one-tape TMs. It refers to the sequence of target states s1,s2,... visited by a TM when its pointer crosses the boundary between a pair of adjacent tape squares. States s1,s3,... are reached when the pointer moves forward and states s2,s4,... are reached when pointer moves backwards. Figure 1 shows how states are visited during a computation and how a crossing sequence is defined.
| # | W | O | R | D | I | N | G | # | # |  | ||
q
0 | q1 | q2 | q3 | q4
| ||||||||
q7 | q6 | q5 | 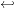 | |||||||||
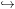 | q8 | q9 | q10 | q11 | … |
Every Hennie machine satisfies, by definition, the property that the length of its crossing sequences is bounded by an integer (Hennie, 1965). Since the finiteness of crossing sequences implies that the TM is equivalent to a finite-state automaton, this bound lets us construct an equivalent finite-state device. The good news is that for all Hennie machines, a bounding constant k is computable (Kobayashi, 1985; Tadaki et al., 2010).
Průša (2014) showed that, if a deterministic Hennie machine recognizing the input language has m states and n working symbols, we can construct a minimal deterministic finite automaton that has 22O(n log m) states. Thus, Hennie machines recognising the input are much more succinct than the equivalent minimal deterministic automaton. Obviously, a deterministic letter transducer constructed from a Hennie machine is not smaller than the minimal automaton recognizing only the input language aka the domain of the transducer.
Now we can prove that Hennie machines can be used, on the one hand, to build a finite-state subset of Generative Phonology using the two-part condition of non-self-application and finite composition, and, on the other, to obtain compilation methods for such grammars that previously required specialized encoding and a compilation algorithm.
Proof. Let R1 and R2 be regular relations and R1′ and R2′ the respective same-length regular relations. Then there are, respectively, two non-deterministic Hennie machines T1 and T2 that recognize R′1 and R2′. The composition R1′∘ R2′ is then computed by a Hennie machine that first runs like T1′, then rewinds the tape and runs like T2′. Since the combined machine preserves the string length, it is equivalent to an epsilon-free finite-state transducer that recognizes the relation R1′∘ R2′. The composition h−1 ∘ R1′∘ R2′∘ h is then equivalent to the regular relation R1 ∘ R2. __
Theorem 2. The non-self-embedding application of rule of the form α → β∕λ_ρ corresponds to a regular relation.
Proof. Extend the original tape alphabet so that each square contains the input letter and a Boolean vector indicating the validity of left and right context conditions of the simultaneous rules. Let ML (MR) be a deterministic (co-deterministic) pattern matching automaton. The state computed by this automaton indicates, for each string position, the type of the prefix (suffix) of the position. Modify this pattern matching automaton by adding self-loops on 0’s. Then transform the automaton into a finite-state transducer ML′ (MR′) in such a way that each transition adds the information on the occurring left (right) contexts to the Boolean vectors of each square. This epsilon-free transducer is a Hennie machine. The composition ML′∘ MR′ is then a Hennie machine that marks the occurring contexts at all squares.
As a pre-processing step, make the length of each left-hand side α and the respective right-hand side β identical by padding the shorter with 0’s. In addition, add synchronous 0’s freely to both. In this way we obtain a letter transducer that recognizes a 0-padded representation of the regular relation α × β.
Define a Hennie machine M1 that sweeps the string (containing 0’s) from left to right and non-deterministically overwrites ranges of squares that contain some left-hand-side string α with a corresponding right-hand-side string β when the first and the last square in the input range indicate the presence of the required left and right context, respectively. Define also a Hennie machine M2 that removes the Boolean context vectors from the tape squares. Now the composition ML′∘MR′∘M1 ∘M2 is recognized by a Hennie machine M. Then h−1 ∘ M ∘ h is equivalent to a non-deterministic finite-state transducer that captures the semantics of the rule. __
We have now used Hennie machines to show that simultaneous non-overlapping rules are regular and that a finite composition of regular rules preserves regularity. Other application modes of regular grammars are discussed in (Johnson, 1972; Kaplan and Kay, 1994). The regularity of these application modes can be proven similarly.
To conclude our argument, we show that Hennie machines actually help us to compile hunspell dictionaries without special encodings.
Theorem 3. The iterated application of monotonic suffix rules of a hunspell grammar makes a regular relation.
Proof. Every suffix rule corresponds to a Hennie machine that backs up checking its context condition and then writes the non-truncated context and the new suffix (4.2-4.3). The union of such Hennie machines is a non-deterministic Hennie machine M. The closure M∗ is a TM that applies suffix rules iteratively. As the suffix rules increase the length of the string monotonically, the closure M∗ has a finite bound for the crossing sequences and recognizes a regular relation. __
The Borodin-Trakhtenbrot Gap Theorem (Trakhtenbrot, 1964) states that expanded resources do not always expand the set of computable functions. In other words, it is possible that the regularity of a TM holds even if the O(n) is made slightly looser. A less tight time bound is now expressed with the little-o notation: t(n) ∈ o(f(n)) means that the upper bound f(n) grows much faster than the running time t(n) when n tends to infinity: limn→∞t(n)∕f(n) = 0.
As an application of the Gap Theorem, Hartmanis (1968) and Trakhtenbrot (1964) showed independently that the time resource of finite-state equivalent deterministic one-tape TMs can be extended from O(n) to o(nlog n). This bound is tight: regularity is algorithmically unsolvable for any bound that exceeds n + 1 in Ω(nlog n) Gajser (2015). The extended time bound has been generalized to non-deterministic one-tape TMs by Tadaki et al. (2010). These extensions of Hennie’s core result give us a new sufficient condition for the regularity of Generative Phonology.
Theorem 4. A generative phonological grammar is regular if its one-tape TM implementation runs in o(nlog n) time.
Let M be a one-tape TM implementation of a generative phonological grammar. The finiteness of the crossing sequences of a given TM is, in general, undecidable (Průša, 2014), but there is a reasonably good decision procedure: To test if M is equivalent to a finite-state transducer, we can pick a function t(n) that is in o(nlog n) and test if M actually runs in t(n). Interestingly, Gajser (2015) showed that for any reasonable function t(n), we can decide whether a TM M runs in t(n). If a TM then runs in t(n), it actually runs in O(n) (Pighizzini, 2009). Thus, the new one-sided condition for regularity of the phonological grammar has a sound approximate solution.
If the suffix rules are non-monotonic and can shorten their inputs, the TM can produce the same configuration again and again and produse arbitrarily long crossing sequences. The repetition may happen either a finite or an infinite number of times. Interestingly, the specialized compilation method (Yli-Jyrä, 2009) handles both cases correctly whereas we fail to get a Hennie machine if the suffix rules are non-monotonic.
Non-monotonic suffix rules are an example of a situation where the TM is equivalent to a Hennie machine that restricts the length of the crossing sequences. The bad news is that we do not know when we have a correct Hennie machine: it is difficult to find such bound k for the length of crossing sequences that a given TM preserves its semantics when longer crossing sequences are abandoned. Since a sufficient bound k is such that the semantics of the restricted TM does not change although we allow longer crossing-sequences, there are reasonable ways to probe possible values of k, but such probing is still heuristic.
The difficulty of non-monotonic grammars indicates that although we now have a more general condition for those generative phonological grammars that are equivalent to a finite-state transducer, a specialized compilation algorithm may still encode infinite loops in a way that seems to be beyond of the Hennie condition.
It is historically interesting that Hennie’s regularity condition dates back to the year 1965, that is even before Chomsky and Halle (1968).
No decision procedure for the classical two-part condition (Johnson, 1972; Kaplan and Kay, 1994), is known. Compared to this situation, it is remarkable that the new sufficient condition has several advantages:
There are many interesting questions that could be studied in the future. Here are some:
There are several potential applications for Hennie machines in Natural Language Processing. We have already demonstrated that Hennie machines have applications in phonology and morphology (Yli-Jyrä, 2009). Weighted Hennie machines may be applied to OCR that is based on weighted context-dependent correction rules (Drobac et al., 2017). Furthermore, non-monotonic Sequential Constraint Grammar is computationally undecidable but has restrictions that have Hennie machine characterizations (Yli-Jyrä, 2017). The search for generative dependency grammars that produce non-projective trees is an area that may also benefit from the concepts of crossing sequences and Hennie machines (Nederhof and Yli-Jyrä, 2017).
Kenneth R. Beesley and Lauri Karttunen. Finite State Morphology. CSLI Studies in Computational Linguistics. CSLI Publications, Stanford, CA, USA, 2003.
J. C. Birget. Two-way automata and length-preserving homomorphisms. Mathematical systems theory, 29(3): 191–226, Jun 1996. URL http://dx.doi.org/10.1007/BF01201276.
Noam Chomsky. Formal properties of grammars. In R. Luce, R. Bush, and E. Galanter, editors, Handbook of Mathematical Psychology, volume II, pages 323–418. John Wiley and Sons, New York, 1963.
Noam Chomsky and Morris Halle. The Sound Pattern of English. Harper & Row, New York, 1968.
Senka Drobac, Pekka Kauppinen, and Krister Lindén. OCR and post-correction of historical Finnish texts. In Proceedings of the 21st Nordic Conference of Computational Linguistics, pages 70–76, Gothenburg, Sweden, 23-24 May 2017. Linkoping University Electronic Press. URL http://www.ep.liu.se/ecp/131/009/ecp17131009.pdf.
Joost Engelfriet and Hendrik Jan Hoogeboom. MSO definable string transductions and two-way finite-state transducers. ACM Trans. Comput. Logic, 2(2):216–254, April 2001. URL http://doi.acm.org/10.1145/371316.371512.
Michael J. Fischer. Two characterizations of the context-sensitive languages. In IEEE Conference Record of 10th Annual Symposium on Switching and Automata Theory, pages 149–156, 1969. URL http://ieeexplore.ieee.org/document/4569611/.
David Gajser. Verifying time complexity of Turing machines. Theoretical Computer Science, 600:86–97, 2015. URL https://doi.org/10.1016/j.tcs.2015.07.028.
Sheila Greibach. A note on undecidable properties of formal languages. Mathematical Systems Theory, 2(1):1–6, 1968. URL https://doi.org/10.1007/BF01691341.
Juri Hartmanis. Computational complexity of one-tape Turing machine computations. J. ACM, 15(2):325–339, April 1968. URL http://doi.acm.org/10.1145/321450.321464.
Frederick C. Hennie. One-tape, off-line Turing machine computations. Information and Control, 8(6):553–578, 1965. URL https://doi.org/10.1016/S0019-9958(65)90399-2.
Charles Hockett. Two models of grammatical description. Word, 10:210–231, 1954.
John E. Hopcroft and Jeffrey D. Ullman. Introduction to Automata Theory, Language, and Computation. AddisonWesley, Reading, MA, 1979.
C. Douglas Johnson. Formal Aspects of Phonological Description. Number 3 in Monographs on linguistic analysis. Mouton, The Hague, 1972.
Daniel Jurafsky and James H. Martin, editors. Speech and Language Processing: An introduction to Natural Language Processing, Computational Linguistics, and Speech Processing. Prentice-Hall, 2000.
Ronald M. Kaplan and Martin Kay. Regular models of phonological rule systems. Computational Linguistics, 20(3):331–378, September 1994. URL http://aclweb.org/anthology/J94-3001.
Christos A. Kapoutsis. Minicomplexity. In Martin Kutrib, Nelma Moreira, and Rogério Reis, editors, Descriptional Complexity of Formal Systems: 14th International Workshop, DCFS 2012, Braga, Portugal, July 23-25, 2012. Proceedings, pages 20–42, Berlin, Heidelberg, 2012. Springer Berlin Heidelberg. URL http://dx.doi.org/10.1007/978-3-642-31623-4_2.
Lauri Karttunen. The replace operator. In 33th ACL 1995, Proceedings of the Conference, pages 16–23, Cambridge, MA, USA, 1995. URL https://dl.acm.org/citation.cfm?id=981658.981661.
Kojiro Kobayashi. On the structure of one-tape nondeterministic Turing machine time hierarchy. Theoretical Computer Science, 40(2–3):175–193, 1985. URL https://doi.org/10.1016/0304-3975(85)90165-3.
Kimmo Koskenniemi. Two-level morphology: a general computational model for word-form recognition and production. Number 11 in Publications of the Department of General Linguistics, University of Helsinki. Yliopistopaino, Helsinki, 1983.
John McCarthy. Harmonic serialism and parallelism. Number 98 in Linguistics Department Faculty Publication Series, Amherst, MA, 2000. University of Massachusetts. URL http://scholarworks.umass.edu/linguist_faculty_pubs/98.
Jens Michaelis and Marcus Kracht. Semilinearity as a syntactic invariant? Logical Aspects of Computational Linguistics, 1328:329–345, 1997. URL https://doi.org/10.1007/BFb0052165.
Karuvannur Puthanveettil Mohanan. The Theory of Lexical Phonology, volume 6 of Studies in Natural Language and Linguistic Theory. Springer Netherlands, 1986.
Mehryar Mohri and Richard Sproat. An efficient compiler for weighted rewrite rules. In 34th ACL 1996, Proceedings of the Conference, pages 231–238, Santa Cruz, CA, USA, June 24-27 1996. URL http://aclweb.org/anthology/P96-1031.
Mark-Jan Nederhof and Anssi Yli-Jyrä. A derivational model of discontinuous parsing. In Frank Drewes, Carlos Martín-Vide, and Bianca Truthe, editors, Language and Automata Theory and Applications - 11th International Conference, LATA 2017, Umeå, Sweden, March 6-9, 2017, Proceedings, volume 10168 of Lecture Notes in Computer Science, pages 299–310, 2017. URL https://doi.org/10.1007/978-3-319-53733-7_22.
László Németh, Viktor Trón, Péter Halácsy, András Kornai, András Rung, and István Szakadát. Leveraging the open source ispell codebase for minority language analysis. In First Steps in Language Documentation for Minority Languages: Computational Linguistic Tools for Morphology, Lexicon and Corpus Compilation, Proceedings of the SALTMIL Workshop at LREC 2004, pages 56–59, 2004. http://isl.ntf.uni-lj.si/SALTMIL/.
Giovanni Pighizzini. Nondeterministic one-tape off-line Turing machines and their time complexity. J. Autom. Lang. Comb., 14:107–124, 2009. URL http://dl.acm.org/citation.cfm?id=1643359.1643367.
Tommi A. Pirinen and Krister Lindén. Creating and weighting Hunspell dictionaries as finite-state automata. Investigationes Linguisticae, XXI, 2010.
Karl Raimund Popper. The Logic of Scientific Discovery. Hutchinson & Co., London, 2nd edition, 1959.
Alan Prince and Paul Smolensky. Optimality Theory: Constraint interaction in Generative Grammar. Blackwell, 2002. URL http://roa.rutgers.edu/files/537-0802/537-0802-PRINCE-0-0.PDF.
Daniel Průša. Weight-reducing Hennie machines and their descriptional complexity. In Adrian-Horia Dediu, Carlos Martín-Vide, José-Luis Sierra-Rodríguez, and Bianca Truthe, editors, Language and Automata Theory and Applications: 8th International Conference, LATA 2014, Madrid, Spain, March 10-14, 2014. Proceedings, pages 553–564, Cham, 2014. Springer International Publishing. URL http://dx.doi.org/10.1007/978-3-319-04921-2_45.
Michael O. Rabin. Real time computation. Israel Journal of Mathematics, 1(4):203–211, 1963. URL http://dx.doi.org/10.1007/BF02759719.
Eric Sven Ristad. Computational structure of generative phonology and its relation to language comprehension. In Proceedings of the 28th Annual Meeting on Association for Computational Linguistics, ACL ’90, pages 235–242, Pittsburgh, Pennsylvania, 1990. URL http://dx.doi.org/10.3115/981823.981853.
Richard E. Stearns. A regularity test for pushdown machines. Information and Control, 11(3):323 – 340, 1967. URL http://doi.org/10.1016/S0019-9958(67)90591-8.
Kohtaro Tadaki, Tomoyuki Yamakami, and Jack C. H. Lin. Theory of one-tape linear-time Turing machines. Theoretical Computer Science, 411(1): 22–43, 2010. URL https://doi.org/10.1007/978-3-540-24618-3_29.
Boris A. Trakhtenbrot. Turing computations with logarithmic delay (in Russian). Albegra i Logica, pages 33–34, 1964. English translation in U. of California Computing Center, Tech. Report. No. 5, Berkeley, CA, 1966.
Anssi Yli-Jyrä. An efficient double complementation algorithm for superposition-based finite-state morphology. In Kristiina Jokinen and Eckhard Bick, editors, NODALIDA 2009 Conference Proceedings, page 206213, 2009. URL http://dspace.ut.ee/handle/10062/9765.
Anssi Yli-Jyrä. The power of constraint grammars revisited. In Proceedings of the NoDaLiDa 2017 Workshop on Constraint Grammar - Methods, Tools and Applications, 22 May 2017, Gothenburg, Sweden, pages 23–31, 2017. URL http://www.ep.liu.se/ecp/140/005/ecp17140005.pdf.